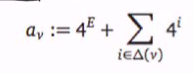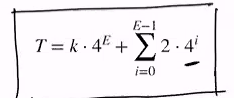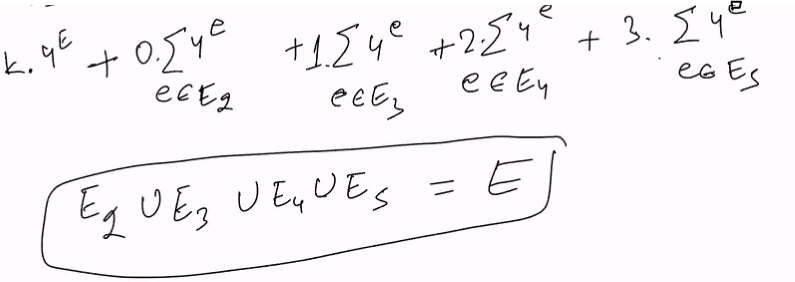Subset Sum

Problem: Given a set X of n numbers, and a target T, decide whether there exist a subset of X that adds to T.

• There is a dp solution
• It is NP hardness because the runtime is not polynormial to the size of the input: n+logT, the dp solution is nT

  We can show NP-hardness

1. Reduce from vertex cover
   • Given G = (V,E) and a number k
2. Produce a set X and number T such that
   • The graph has vertex cover of k
   • This implies that the set X has a subset that adds to T
   • There is a subset of X that adds to T implies that the graph has a vertex cover of size k

Corresponding:

• Vertex cover: Subset of vertices that covers all edges of size k

• Subset sum: Subset of numbers that adds to T

Perhaps we can let one edge be a number and that T is the sum of these numbers. But then there might be many different ways to add up a number to get another number, so we can pick this edge to be a representation in different digits

Reduction

• Number the edges arbitrarily from 0 to E-1
• Our set X contains the integer bi := 4^i for each edge i and the integer:

for each vertex c where the sum of v is the set of edges that have v has an endpoint

For every vertex look at the neigbouring and add 4^i to these vertices where i is the weight

• 4 is an arb number large enough so that the contribution of different edges do not get “,mix up” when adding these number.. We could have choosen 10 as well

• Should cover all edges
• Each edges can only appear once or twice (Depending which vertices was added up)

If the graph has an vertex cover of size k, then there exist a subset of x that adds to T

X = {be : e exist as an Edge} U {av: v exist in V}, such that be = 4^e, a = e^E + sum of be

T = k . 4^e + 2(4^0 + 4 + …. 4^E-1)

• Let v1.. Vk be vertex cover
• av1..avk is T
• Notice that this means 4^E * k + summation of be + sum of be’
  • There are some subset of the edges where we added them twice because both vertex are in the vertex cover (be’)
• Every edge has been added at least once

Other direction

Suppose there is a subset of X that adds to T

• {av: v exist in V}
• {be: e exist in E}
• T = k * 4^E + 2 * sum of be

Let X1 be a subset of X that adds to T

• X1 = {av: v is a set of V1} U {be: e exist in E1}

Claim 1:

• The size of V1 is at most k (V1 <=k)

Proof: Suppose it is not k

• Remeber that T = k*4^E + 2(4^0 + …4^E-1)
• Then sum of av is greater or equal to (k+1) * 4^E
• then T = k * 4 + 2(4^E -1)
• But then.. it is less than what we said.. which is not possible

Claim 2:

• The size of V1 is at least k (V1 >= k)

Proof:

• Suppose V1 <= k -1
• Then sum of av + sum of be where the values of v and e are in V1 and E1
• Then we realised that (k-1) * 4^e + 3(4^0 + 4 + ….4^E-1)

Claim 3: V1 is a vertex cover

• The sum of av + sum of be where e and v are in E1 and V1
• This equates to k*4^E + 2(4^0 + 4 + … 4^E-1)
• sum of av matches k*4^E
• This also meant that the sum of 2 * (4^0 + 4 + 4^2 … 4^E-1) = 0 (Sum of E^e in E2) + 1 (Sum of E^e in E3) + 2(Sum of E^e in E4) + 3 (Sum of E^e in E5)
• This meant that only E4 has values and the rest is 0
• This means that E4 is E

• 2(sum of 4^e) where e is in E = (sum of 4^2, where e is in E1) + (sum of av, where v is in V1)

• Why does NP hardness proof not imply that P=NP
  • T is not polynomial in the size of our input

Partition problem

Problem: Given a set X of n numbers, find a partitioning of X into X1 and X2 such that the sum of elements in X1 and X2 is the same

• Theory: NP-hard
• Reduce from subset-sum

Given a set of numbers X such that the sum of all elements in X is S, we want to add two large numbers P and Q to the set S such that X union {P,Q} can be divded into two sets with equal sum iff X can be divided into two parts that add to T and S-T

Hamiltonian Cycle problem

• A hamilitonian cycle in a directed graph is a cycle that visit every vertex in the graph exactly once

Problem: Given a directed graph G = (V,E), does there exist a hamiltonian cycle

Reduction

• Reduce from 3-SAT or from vertex cover to show NP-hardness
• Reduction is tricky
• Use NP hardness of HC to talk about other problems

All NP-complete problems are polynomial time reducible to each other. Not all reductions are easy to find Sometimes it is easier to reduce from A to B and then B to C instead of A to C directly

Hamiltonian Path Problem

• HP from s to t in a directed graph is a path that begind with s and ends at t and visit every vertx in the graph exactly once

Problem: Given a directed graph G = (V,E) such that does there exist a Hamilitonian path from s to t

Theorem: It is NP-hard

• Reduce it from hamiltonian cycle
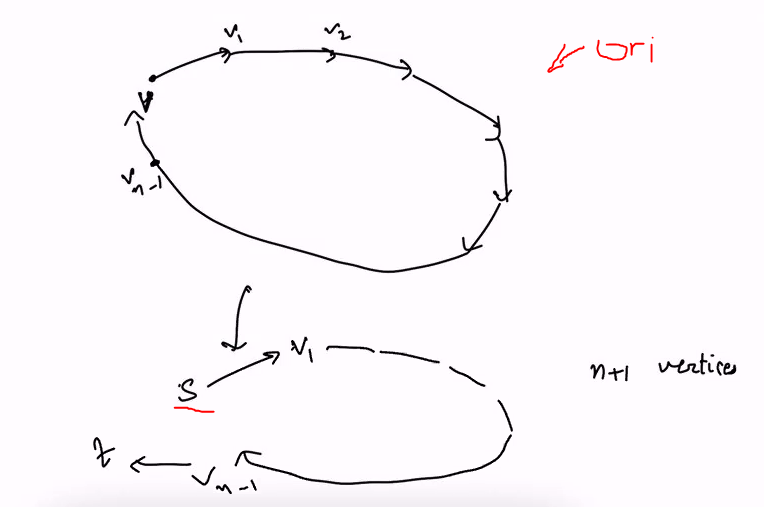
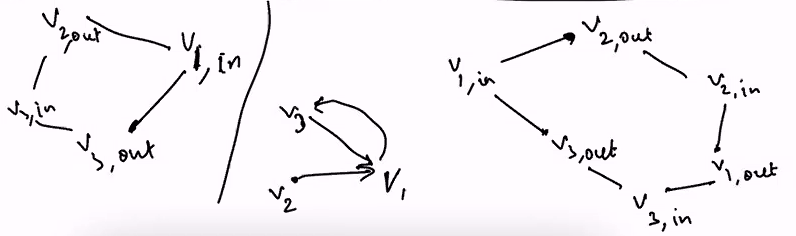
• Given G = (V.E) choose arbitrary vertex v in G
• Replace v by two vertices s and t and add (s to u) for every edge (v to u) in G and add (u to v).
  • t represent incoming vertices to v
  • s represent the outgoing edges from v

Reason

If there is a hamiltonian cycle, lets look at one vertice in this cycle call v

Our modified graph

It will start at S because S is the start of the direction and it will end at t since its the last value.

There is a cycle because t is the ending vertex and it starts at s again. We show that this graph can be changed into jus a HamPath by transforming it into this new graph

Remarks

• NP-complete problems are poly time reducible to each others
• Not all these reductin are easy to find

Undirected Hamilitonian Cycle Problem

Problem: Given an undirected graph G = (V,E) does there exist a Hamilitonian cycle

Reduce

• Reduce it from Directed Hamilitonaian Path
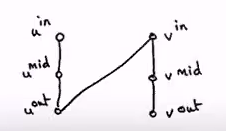
• For each vertex v, we add tree vertices uin, umid, uout
• For every edge, (u to v), (outgoing) we add the following edges

This means any cycle that goes throguh the vertice it must be taking this path

Proof to this:

• There exist a ham cycle in this undirected graph
• The ham cycle is v1in - v1mid - v1out - v2in - v3 mid …… vnin - vnmid - vnout - (go back) vin

  This is cycle with 3n vertice

Suppose there is a ham cycle in the modified graph G’,

• For any v in V,
  • Notice that Vmid must be connected to Vin and Vout
  • This implies that in the new graph, we must include vin, vmid and vout
• We also know that v1out must be connected to a v2in
  • All the out vertex must be connected to the in vertex
• Since its a ham cycle, we know that v2mid must be connected to v2in and v2out,
  • We can see it will continue connection until it reach vnin - vnmid - vnout
  • Eventually it will reach back v1in
  • Since its a ham cycle,m it must have exhasted all the vertex before coming to v1in

Why need the mid vertice?

• Imagine the construction of a graph that does not make use of vmid
• Mid vertex force that the graph looks like this

Claim: The original undirected graph was a HamCycle iff the new undirected graph has a HamCycle

Traveling Salesman problem

Problem: Given a list of cities and the distance between each pair of cities, what is the shortest possible route that visit each city and returns to origin city

• Does there exist a town of length less than or equal to k

  This is similar to the Undirected Hamiltonian cycle problem, except that it is on a weighted graph

Theorem: TSP is NP-Hard

reduce it from undirected Hamiltonian Cycle

NP hardness of search Optimisation problem

A search problem cannot be in NP but can be in NPhard

• NP is define to be a class of decision problems

• If a known NP-hard problem can be efficiently reduce to A (which is a search/optimisation problem) then this shows that A is NP-hard
• A search/optimsation cannot be NP complete. For A to be NP-complete, it should be in NP which is only well defined for decision problems

Approximation Algorithm

• we dont know how to solve np-complete
• Get something close to this
• Approximate the solution
  • Say find an assignment of a 3 SAT instance that satisfies 90 percent of the clauses
  • Or find a path for a traveling salesman that is 110 percent of the best path
• This is good enough for most application

Even some problems, it is hard to get the approximate

TSP is NP hard to approximate

• Consider edge weighted undirected graph G. Let the minimum length of a tour of the graph G starting with vertex v and ending with vertex v is M

Problem: c-approximate TSP: Our task is to find a tour starting and ending with vertex v and total length cM for some c>1

Theorem: c-approximate TSP is NP-hard

• reduce from undirected Hamilitonian cycle problem

• Create a new complete G’ = (V,E’) with edge weight defined as w(x,y) = 1 if (x,y) is in E and w(x,y) = cn +1 otherwise
  • Weight present in original, assign as 1 else assign as some hughe weight
• G has a hamiltonian cycle iff G’ has a cycle with total weight n iff G’ has a cycle of total weight at most cn
• Either we have 1 or cn+1, if we choose cn+1, then the weight will overexceed
• Getting the solution is just as hard as apporoximating it

Euclidean TSP problem

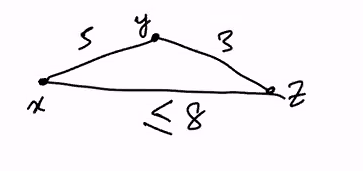
Problem: This is the TSP problem with the additional restriction that for any three vertices x,y,z, w(x,y) + w(y,z) >= w(x,z) ie the distance from x to z is at msot distance of going from x to y and then going from y to z

This proof is hard

Efficient Algorithm for 2-approximate EuclideanTSP

• Use min span tree

To approximate the smallest tour P starting with vertex v.

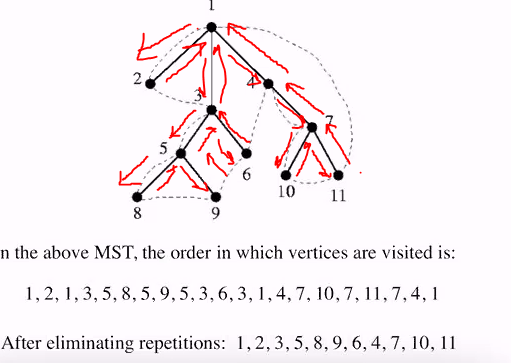
• Let T be the minimum spanning tree for G. Consider T as a tree rooted at v.
• TSP(T,v)
  • Add v to P
  • For each child u of v - TSP(T,u)
    • Add v to P
• Remove all repeated appearance of any vertex in P

• Every edge is visited twice
• w(path) is 2 * w(MST)
• The claim is that the weight will only go down adn not up
  • When we eliminate a vertex, we will replace a vertex w(2,1) + w(1,3) to w(2,3) where w(2,3) is less than or equal to w(2,1) + w(1,3)
  • If we keep doing these eli, the total weight is always decreasing
  • This satisfy the euclidean property

Why does it work

Show the following observation that lead to the proof

• The min spanning tree is the smallest connected graph spanning all vertices. So the total weight is less than the total tour weight of the travelling salesman
• Our algo visit every edge of the tree exactly twice withut the last step
• By removing repeated appearance of vertices in the last step, we only decrease the total weight of the tour (This uses the Euclidean property)

2 Approximation Algo for vertex cover

Problem: Given an undirected graph G = (V,E) find a subset of vertices V’ that covers each edge in G and is at most twice the size of the smallest vertex cover

Algo:

• While there exist an edge (u to v) not covered by V’
  • Add u,v to V’
• Correctness is immediate from the fact that for any vertex cover V’’, and for any pair of vertices u,v added to V’ in any single step at least one of u, v must be in V’’

Slide