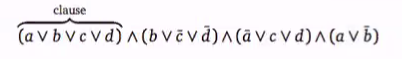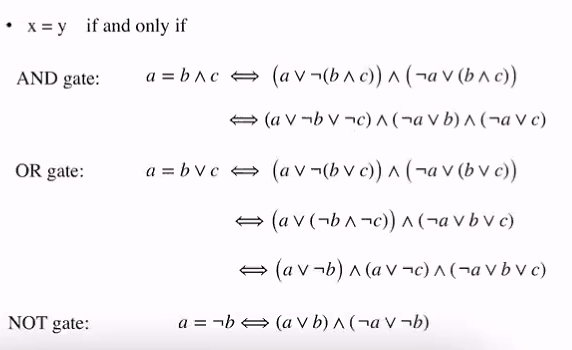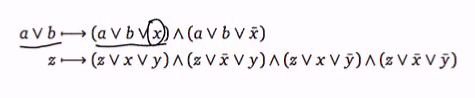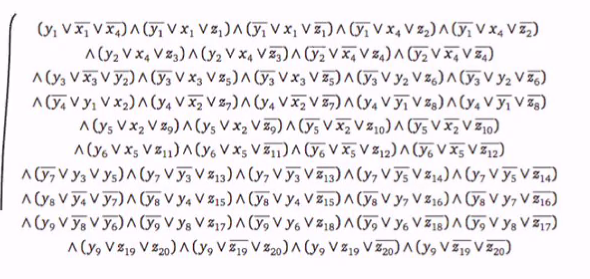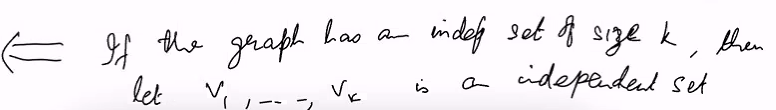A game you can’t win

• Imagine an adversay present you with a black steel box with n binary switches on the front and light bulb on top
• Sales man tell you that the state of the light bulb is controlled by a complex boolean circuit and a collection of AND, OR and NOT gates connected by wires, with one input wire for each switch and a single output wire for the bulb

Can you set the switches so that the light bulb turns on?

• Try different combination
• Say if there is existance combination

No matter what the answer, the salesman can produce a circuit that is inconsistent with our answer unless we had tried all 2^n

Showing you the circuit

• No
• Circuit Sat problem
• Given X1.. Xn, it is easy to check whether they satisfy the circuit in time linear in the number of gates
• But no one knows any algo that givern the circuit as inpyt tells whether there exist x1..xn satisfying the circuit

No one knows if this is impossible either

Recalling reduction

Reduction: Input for A -> Input for problem B -> Use algo for B to solve -> Solution for A

• Problem A reduces to B if efficient algo for B implies an efficient algo for A.
  • Squaring integers reduces to multiplying integers
  • Median finding reduces to finding kth smallest element given k
  • APSP reduces to APSP with no negative weights (JOhnson)
• A reduces to B implies:
  • If B is easy the A is easy
  • If A is hard then B is hard

polynomial time is efficient

1. A - n^2 -> B - n^3 -> C
2. A - n^c -> C

• Efficient means polynomial time, meaning the input
• Computational complexity theory:
  • Compososable: A reduces to B in poly time and B reduces to C in poly time then A reduces to C in poly time
  • In practice, an n^100 algo for any realistic problem usually means another n^c time algo for some small constant c

P vs NP

A decision problem is a prob whose output is a single boolean value: Ues or no

• P: Set of decision problems that can be solved in polynomial time. Intuitively, P is the set of problems that can be solve quickly
• NP: Set of decision problems with the following property:
  • If the answer is yes, then there is a proof of this fact that can be checked in polynomial time - Given a circuit, decide if ther exist x1 to xn such that C(x1..Xn) = 1
    • In this case, x1..xn is the proof
  • NP is the set of decision problems where we can verify a Yes answer quickly if we have the solution in front of us
• co-NP: The opposite of NP. If the answer to a problem in co-NP is No, then there is a proof of this fact that can be checked in polynomial time
  • for all forall x_1 to x_n, –> C(x_1 to x_n) = 0?

We do not know if ckk-sat is co-NP: - There is no other way than to check every single combination

It is easy to see circuit-sat is in NP: a satisfying assignment is a proof.

• We dont know whether circuit sat is in P
• We dont know if its in co-NP either

  There is no proof that tell us that the circuit is not satisfiable

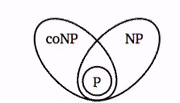
NP and CO NP

• P is contain in NP
• NP is contain in CoNP

Given n, k does there exist a factor of m that is less than or equal to k

• This is similiar to the factorial problem
• The proof:
  • Yes: (NP) factorisation of factor n

    We dont know if its P

NP hardness and NP completeness

• A problem P is NP-hard if it is at least as hard as any problem A in NP
• Problem P is NP hard if for any problem A in NP
  • There is an efficient reduction from A to P
  • If we can solve P, then every problem in NP can be solvable
• If P is NP hard and P is in NP then P is NP-complete

Circuit SAT is NP-complete

• Start with arb problem A in NP and show efficient reduction from A to circuit Sat
• Proof is difficult

Prove NP-hardness

• If there is an efficient reduction from P to A and
  • We know P is NP-hard, then this means that A is NP-hard

TO prove the problem A is NP-Hard, reduce a known NP-Hard problem to A

Reduce Cicuit-sat to A, then a polynomial time algo for A will imply a polynomial time algo for circuit-sat

• Which imples a polynomial time algo for all of NP Hence shows that A is NP-hard

Hardproblems

• Circuit Sat is harder than any problem in NP
• P, reduce circuit sat to P
• This establish P is hard
• Q, reducing P to Q establish that Q is hard

Analogy

• Wresting competition among all problem sin NP and each problem is trying to prove that they are the best (read hardest)
• Efficient reduction from A to B means A looses to B (Read B is at least as hard as A) The first wrestler to establish as being the best hardest in the world of problems in NP needs to win against everyone in the world
• We know that circuit sat already established itself in the 70s as the best
• This is done by reducing every problem in NP to circuit sat
• Any new wrestler just need to defeat the best(Hardest) to be established as the best

To prove NP-hard of A, we only need to give a reduction from an already established NP-hard problem to A

REMARK: All NP - Complete problems can be reduces to one another and are hence equally hard

Cook reduction vs Karp Reductions

• A cook reduction is a poly time reduction from problem A to B
• Karp reduction is specialised reduction where, given an input x to problems A, we prodice an input f(x) to problem B such that
  • If problem A on input x output YES, then problem B on input f(x) output YES
  • If problem A on input x outputs NO, then problem B on input f(x) output NO.
• We will not worry about this distinction, all reduction we will see are actually KARP reduction though.

3-SAT

A boolean function is inconjunctive normal form (CNF) if its a conjuction of several clauses, each of which is the disjunction (or) of several literals, each of which is either a variable or its negation. (This is an and of ors)

• A 3CNF is a CNF where each clause has exactly three literals
• The above is not a 3-CNF since 1st clause has 4 literals and last has two literals (The brackets must have 3)
• Check if there is a value of a,b,c,d such that the entire statement reduces to 1

3-SAT problem: Given a 3-CNF, is there an assignment (Values of the boolean variables) that makes the fomula evalute to TRUE

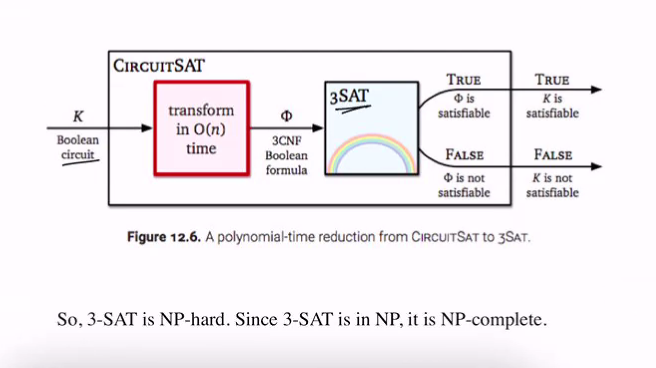
CKTSAT -> 3 SAT

• If 3-sat is easy, this means that we can use that algo to solve circuit sat
• Ckt - sat is hard means that 3sat is hard

Contrapostive are always true if the positive is true

3-sat is NO hard and “” in NP = > 3 sat is NP complete

Circuit-SAT to 3-SAT reduction

• Given c, construct 3-cnf Q such that there exist an x such that c(x) = 1 if and only fi there exist an x such that Q(x) = 1
• We express x=y as a boolean formula in CNF as follows:

x = y if and only if (x or notY) and (notx or y)

So we can transform every gate into at most-3 clauses

• Changing 1 clause and 2 clause to 3 clause with auxiliary variables

if a or B is true, this means that a or b or x is true AND a or v or notx is true

For every clause, we introduce fresh auxilar variables. For each gate, we create a constant number of claises

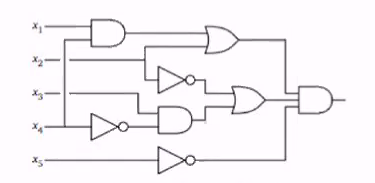
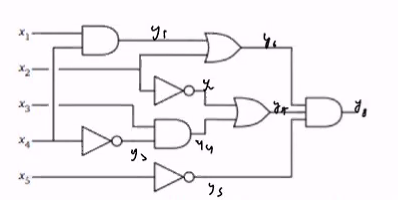
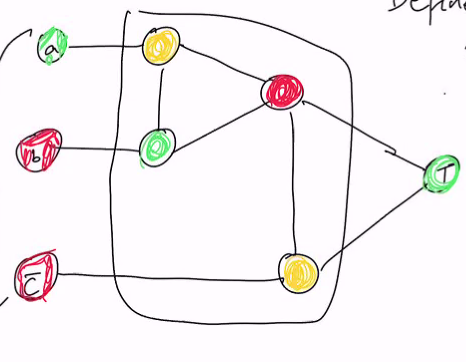
Example

• For the following circuit:

Our reduction will give the following 3-SAT formula

• y1 = x1 and x4
• y6 = x2 and y1
• Until y8 = 1

This is only larger than a factor of 5

3-Sat is NP hard, since its in NP, it is NP complete

SAT

• A canoical example: Consider the formula satifiability problem, usually just called SAT. The input to SAT is a boolean formula like

Remark: 2 Sat is solvablein polynomial time

A 3-SAT function is a special case of general SAT formula. So there is a trivial reduction from 3SAT to SAT. Just return the original formula

Conl: SAT is NP-hard

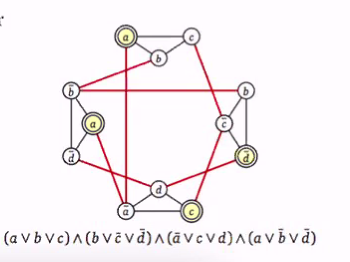
Maximum independent set

• Let G = (V,E) be arbitrary undirected graph
• An independent set in G is set of vertices V’ is a subset of V such that there is no edge between any two vertices in V’
• MaxIndSet Problem: Given G = (V,E) and k>0 as input, does there exist an independent set of size of least k.
• the proof here is the set of vertices

Prove NP-hardness by reducing 3-SAT

Given 3-SAt instance with k clauses, define a graph with 3k vertices where for each literal in each clause, we introduce a new vertex

Two vertices in G are connected by an edge if they either - Correspond to literals within the same clause - Are negation of each others

• take the first clause and create a 3 cnf
• Connect a vertex to varaible and its negation

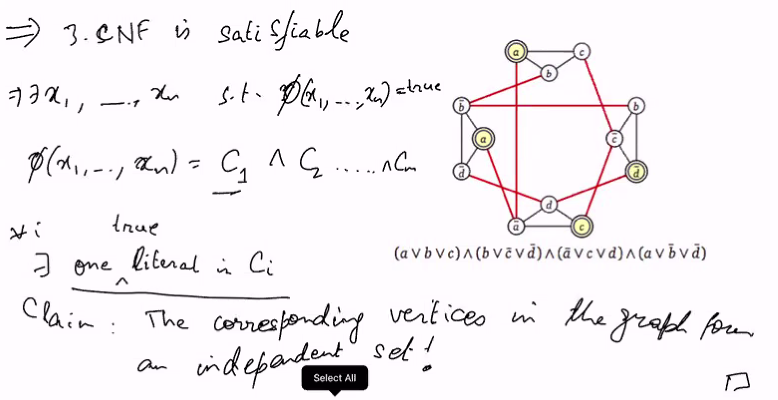
Theorem:

• The graph has an independent set of size k, if and only if the the 3-CNF is satisfiable

• For each of these vertices, set the corresponding literals to true, this will nto cause conflict because the vertices are not connected
• For remain varaibles that are not set to true, pick a value arbituary

Reducing 3sat to independence sat

• For any 3sat formula, construct an instance of independence sat which is G = (V,E) and INDEPDENENT SET OF SIZE k
• Reduction is one direction only (We are nt doing indep set to 3sat)
• If have size k, then is reducable

  General pattern

  

Clique and vertex cover

• MAXCLIQUE: Given undirected G = (V,E) and positive integer k does there exist a subset of vertices V’ of size at least k that forms a clique (All pairs of vertices in V’ connected by an edge)
• Vertex cover: Given undirected G = (V,E) and postiive integer k, does there exist a subset of vertices V’ of size at most k, such that for all edges (u,v) in E either u or v is V’

We know that Max independent is already NP hard, can we reduce max independence sat to this problem as well

• Take the complement graph

MAXCLIQUE IS NP HARD

• Just consider the complement graph. If G jas an independent set of k then G’ has a clique of size k

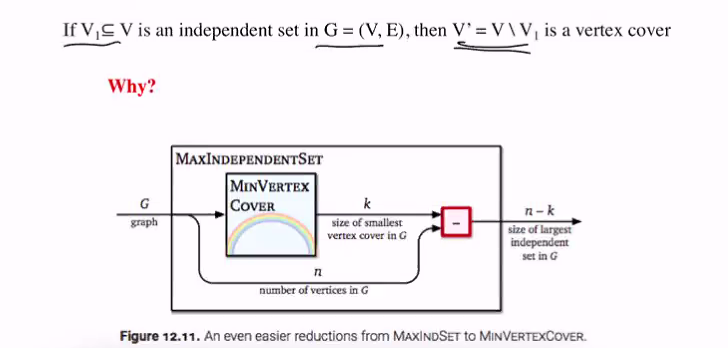
Vertex cover is NP-hard

• If V1 is a subset of V, is an independent set in G = (V,E) then V’ = V\V1 is a vertex cover
• Refer to the picture, thje vertex in this graph is the complement of maxclqie

CLAIM: G has an independent set of size k if and only if G has a vertex cover of size n-k

• v1 to vk are independent
• remaining vertex u1 to u1k, is a vertex cover
• Consider any edge (x,y), both x, y are not in V1.
• This implies that edge (x,y) is covered by v2

Other direction:

• If this is vertex cover
• Consider that any pair of vertices vi, vj in v1
• CLaim: They cannot be connected by the edge because we say that they are in vertex cover

Graph 3 - coloring

A proper k-coloring of a graph G = (V,E) is function C: V-> {1,2…k} that assigns one of k “colours” to each vertex, so that every edge has two different colour at its endpoints

• Graph colouring problem ask for a colouring of a graph with minimum number of colour
• 3 Colouring problem: Given G = (V,E).. Does there exist a proper 3-coloring

Reduction

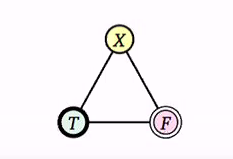
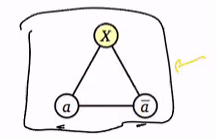
• Before looking at 3-sat intances, we begin by creating a triangle (3-Clique) and label the vertices T,F,X. Note that in any proper 3 coloring, these will be assigned different colour
• We want to find an assignment if an only if there exist the coloring, the coloruing must satisfy all the different edges
• Without loss of generality, we assume the colours are shown below
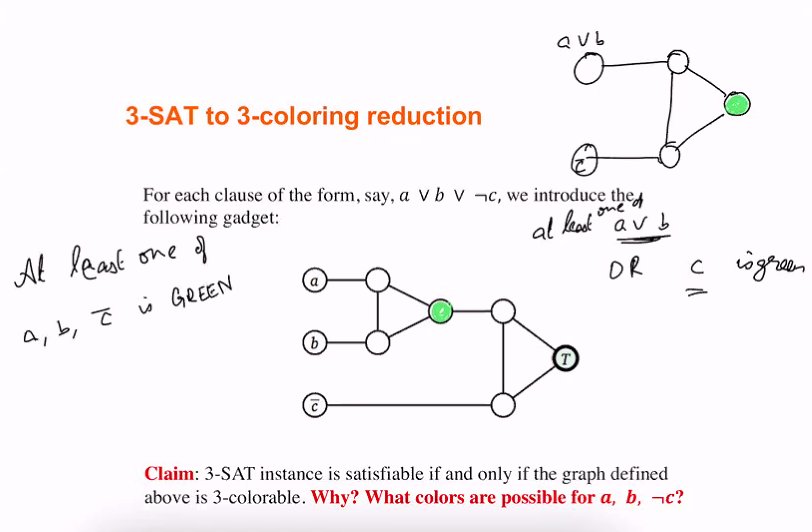
  • for each clause, we will create a small graph g*
  • The clause is only true if and only if g* is 3 colour label
  • Look at a or b: This is true when one of a, b is coloured green
  • the center two nodes is either red or yellow but both cannot be same colour
  • At least one of a,b is green

• Introduce the following 3 cliques in our graphs

• This already indicate how the coloring will be related to the assignment

• For each clause of the form, say avbvnotc we introduce:

• If there is a valid colouring, At least one of the first 3 nodes are either green or pink (Never yellow)

Correctness

Proof: If the formula is satisfiable, then there exist a valid 3 colouring..

• For any satisfying assignment, True implies green, False implies Pink
• This means at least one of the starting nodes will be green colour
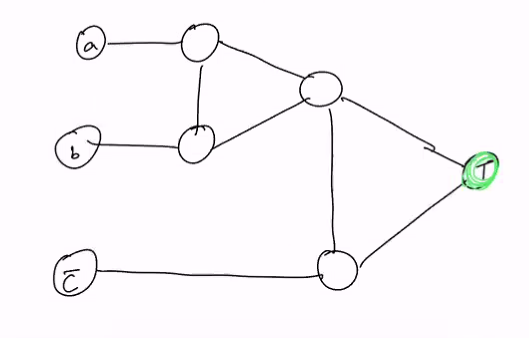
• There are 7 possibilies

For example, we could have green, red, red Then the graph must look like this

The centre’s colouring is correct

How is it related to SAT?

• SAT: satisfy the formula where one of the variable is true
• Colouring: Satisfy the same formula where one of the variable is green

In this case we are taking green to be the equivalent to true in SAT

If we are force to have all be red,

It doesnt work

If the graph has a valid 3 colouring then the formula must be satisfiable

1. Get problem A’s algo (3 Colouring algo)
2. Run function F on this algo to get a graph (Change the graph to 3 colouring)
3. Running problem B’s algo on this graph to get the solution to A (Running 3 sat algo shows it to solve it to 3 Colouring)

This proofs

Slides