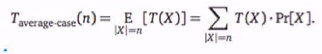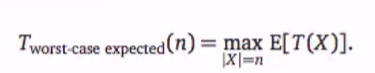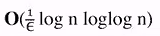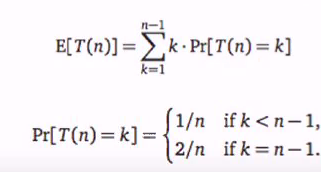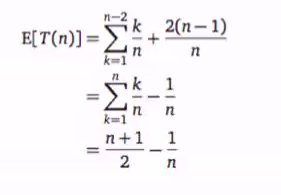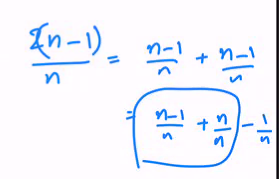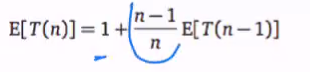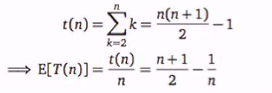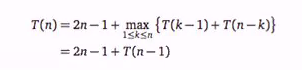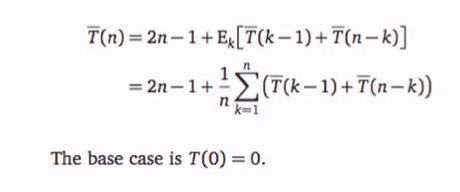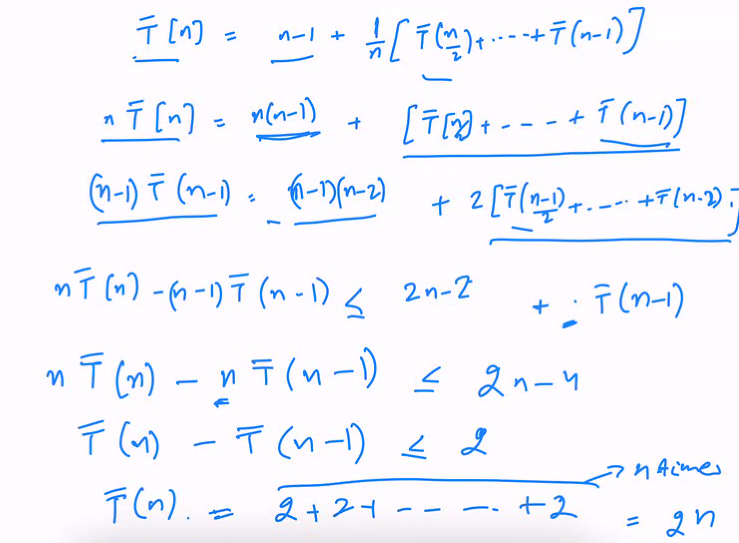Recap:

• Linearity of expectations
• Independent Events
• Conditional probability
• Exclusive Events

Determinstic vs Randomised Algothims

The average case running time is defined by the expected value over all inputs X of a certain size, of the algorithms running time for input X:

• There is an assumption on the input

Worse case Input:

We should still look at the randomnised algorthims worst case. But sometimes by introducing randomness, we can decrease the worse case time

Determinisitc Algorithms

The output as well as the running time are functions only of the input

Randominised Algorthims

The output as well as the running time are functions of the input and random bits

• The output depends on the input as well as the randomness introduce by the algorthim

Example: Approximate Median

Given an Array A from 1 to n, find an element whose rank is in the range [(1-e)n/2 , (1+e)n/2]

A random algo:

1. Select a random sample S of O(1/e lgn) elements of A
2. Sort S
3. Report the median of S

Running time:

The output is an e approximate median with probability 1-n^-2

If N is 10^9 and you sample a small number say 1000, the median would be very close to the actual median. This is a application of chennoffBound.

Example: Nuts and Bolts

Suppose there are n nuts and n bolts of different sizes, with each nut matching exactly one bolt

• We cant tell which is bigger without comparing a nut with a bolt
• How quickly can we match the nuts to the bolts?

Naive: Compare all nuts with all bolts : O(N^2)

Consider: Searching for a matching bolt

• Naive: Test out bolt with every nut (Requires n-1 test in worst case)
• Randomly sample (Succeed in half the number of test)

Analysis

• Look at the problem of finding a nut that matches a given bolt
• Suppose we pick a random nut from untested nuts
• So if k nuts are left to test, each is chosen w.p 1/k

We are producing a random permutation

• E[T(N)] is the expected running time
• T(N): The num of test

1/n is the probability of expectancy.

Expected running time

Using:

Recursive algorithm

• When T(1), 0

• Else recursively find:

  • If we are unable to match the current bolt, we have to try out the other bolt from the remaining pile (Hence the n-1 in E)

To get the solution, define a new function t(n) = nE[T(n)] and rewrite: - t(1) = 0 t(n) = n + t(n-1)

Recurrance:

Finding all matches

We have n nuts and n bolts, we want to match all the pairs…

• Trivial algorhtims requires n^2 comparisons
• Choose a pivot bolt and test it against every nut
• Then test the matching pivot nut against every other bolt
• After 2n-1 comparisons, we have one matching pair and the remaining are partition into two sets: Smaller and larger than matching pair (quick sort)
• The worse case recurrence:

T(N) = O(N^2)

The probability of finding a matching pair as the pivot is 1/n

Equivilance to sorting

• Matching nuts with bolts is similiar to sorting the bolts and nuts according to their sizes in a sense
• If we can sort bolts in O(nlgn) time, we can just do binary search for each nut and match them all in O(nlogn) time (n * binary search)
• In the other direction, if we can match nuts with bolts in O(nlogn) time, we could use merge sort to sort the nuts according to their sizes in O(nlogn) time.

We cannot use merge sort if they werent matched since we are only allowed to compared nuts with bolts and not nuts with nuts. We need to see the matching pairs of bolt and nuts in order to compare if a bolt matches a nut better than the other pair (Hence we cant do nut to nut comparison)

• Pretend we are matching nuts and bolts in nlgn time
• Merge sort and heap sort does not work in this case
• Raandomise quicksort algo (Which is similiar to nut and bolt matching) is much faster than mergesort and heapsort in practice

Choosing pivot at random: Analysis

• Tbar(n) is E[T(N)]

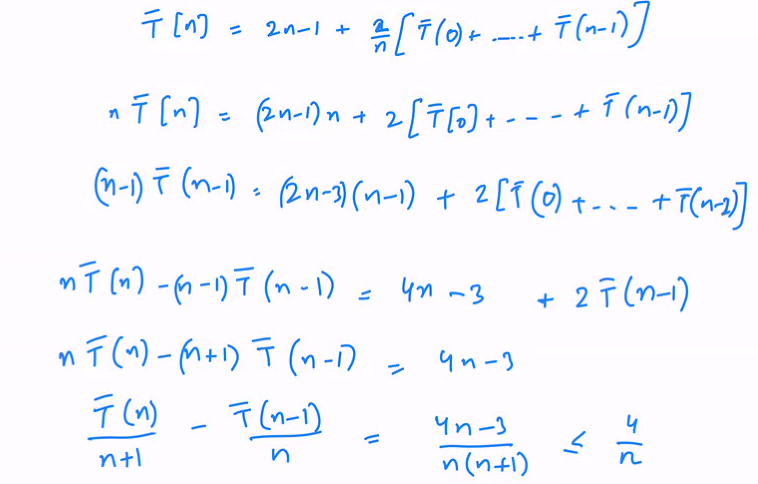
This shows that T(N) is upper bounded by 4T(N+1)(lgn)

Randomised quicksort

• Choose random element as pivot p
• Partition elements smaller than p and larger than pn as A[1..r-1] and A[r+1..n] where r is the rank of the pivot and A[r] = pivot
• RandomisedQuicksort both side

Its similiar to matching nuts and bolts

Randomised Quick select

Not sorting but finding the kth smallest element…

• Choose a random element as pivot p
• Partition elements smaller than p and larger than p as A[1..r-1] and A[r+1..n] where r is the rank of the pivot and A[r] = pivot
• If k = r, return A[r]
• If k<r, then randomisedQuickselect(A[1..r-1], k)
• If k>r, then randomisedQuickselect(A[r+1..n], k-r)

Analysis this to show that it is similiar to nuts and bolts

• Change to less than on equal to handle even / odd numbers

Type of randomised Algorhitms

• Randomised las vegas:
  • Output is always correct
  • Running time is random variable
  • Example: Randomised quick sort, randomised quick select

(assignment problem)

• Randomsied monte carlo algorhtims
  • Output might be incorrect with some probability
  • Running time is deterministics
  • Example: Randomised algorhtims for approximate median

Main motivation for randomised algortihms

• Almost always simpler and faster than the corresponding deterministic algorthims

Example: Quick sort

• Best deterministic algorithms: Mergesort, Heapsort
• Best randomised Algorthims: Quicksort
• Quicksort outperforms both mergesort and heapsort in practice

Example: Smallest Enclosing Circle

Problem: Given n points in a plane, compute the smallest radius circle that encloses all n points

Application such as facilities location

• Determinisintc algorthms: Uses advance geometry and complicated (Runs in O(N) time)
• Best randomised algorthim: Simple algo using elementary geometric (Runs in O(N) time)

• Remove one point
• test if the remaining is within the circle
• If i have 3 points on the boundary, we known there is a unique circle that pass in these 3 points
• Random: We will find these 3 points randomly

Example: Primality Testing

Given an n-bit integer N, test whether N is a prime or not. - Application: RSA

• Best deterministic algorthim:
  • Complicated algo: Time complexity O(n^6), never use
• Best randomised:
  • Simple algo O(n^2)

if n is prime, x^n-1 = 1 mod n

• Pick random a
• Square it
• Check if there is a -1 or +1
• IF there is no -1 or 1 and we end up with a 1, that means it is composite

Example: Generate large prime

Given k, sample a k-digit prime number - Application: RSA

• No deterministc algo
• Obv randomise algo:
  • Sample a k digit number at random and use the density of primes (Prime number theorem)

Slides