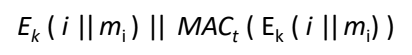Strong authentication

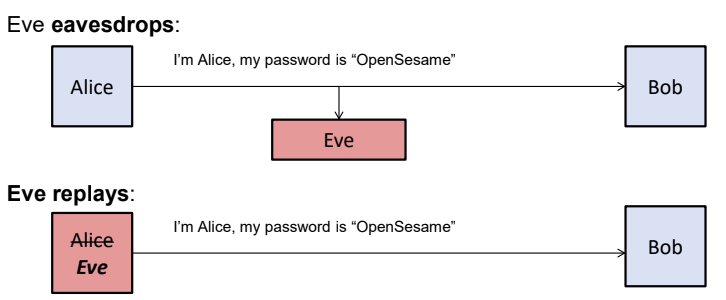
Password is weak authentication: Any eavesdropper can get the password and replay it.

• The password: The secret shared and exchanged between Alice and Bob
• Is it possible to have a mechanism that ALice can prove to Bob that she knows the secret without revealing the secret

SKC Bashed Challenge response

Suppose Alice and Bob have a shared secret key k, and both of them agree on an encryption scheme say AES

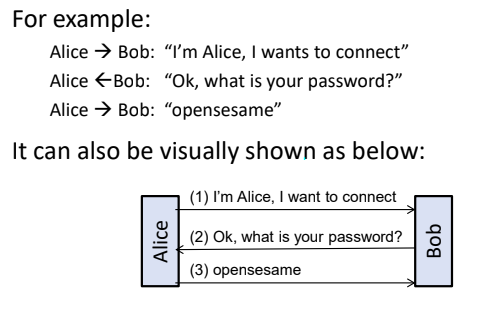
1. Alice sends Bob a hello message
2. (Challenge) Bob randomly picks m and send to Alice: y = Ek(m)
3. (Response) ALice decrypt y to get m and then sends m to Bob
4. Bob verifies that the message received is indeed m is so accepts other wise rejects

• Even if Eve can obtain the communication between Alice and Bob, he cant get the secret key k
• Eve cannot replay the response either: challenge m is randomly chosen and likely to be different in the next authentication session
• The protocol only authenticates alice: Unilateral authentication
• There are protocols to verify both parties: Mutual authentication

What is freshness in the context of authentication protocol

Using PKC:

1. Alice sends Bob a hello message
2. (Challenge) Bob choose random number r and send to Alice: “ALice, here is your challenge, r”
3. (Response) ALice use her private key to sign r and sends to bob: Sign(r), Alice’s certificate
4. Bob verifies Alice’s certificate, extracts Alice’s public key from the certificate then verifies that the signature is correct

• Eve cant know nor derive Alice private key and replay the response because the challenge r is likely to be different
• The value r is also known as cryptographic nonce

The shown protocol have omitted many details, designing a secure authentication protocol is not easy

Is authentication alone sufficient

• There might be mallory who can modify messages and want to pretend to be ALice

• After Bob is convinced that he is communicating with ALice, Mallory interrupts and takes over the channel whilst pretending to be Alice

• Strong authentication: Assumes Mallory is unable to interrupt the session
• For applications whereby Mallory can interrupt the session, we thus need something more

• The outcome of the authentication process must be the new secret k (Session key) established by Alice and Bob

• The process of establishing a secret between Alice and Bob is called key exchange, key agreement, key establishment
• Subsequent communication between Alice and Bob must be secure using the session key which is established by alice and bob

Key exchange and authenticated key exchange

Using a key exchange protocol such thateve is unable to extract any info of the established key

• Cipher
• MAC

  Consider only Eve who can sniff and not mallory who can modify the communication

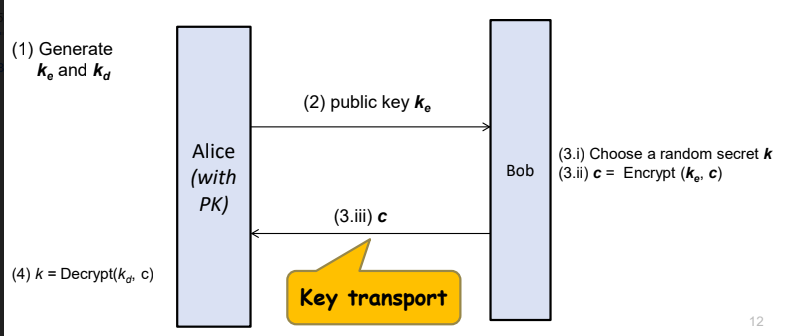
PKC based Unauthenticated Key exchange

1. Alice generates a pair of private and public key
2. Alice sends the public key ke to bob
3. Bob does:
   • Randomly choose secret k
   • Encrypt k using ke
   • Send ciphertext c to Alice
4. Alice use her private key kd to decrupt and obtain k

Basic/Unauthenticated Diffie-hellman Key Exchange

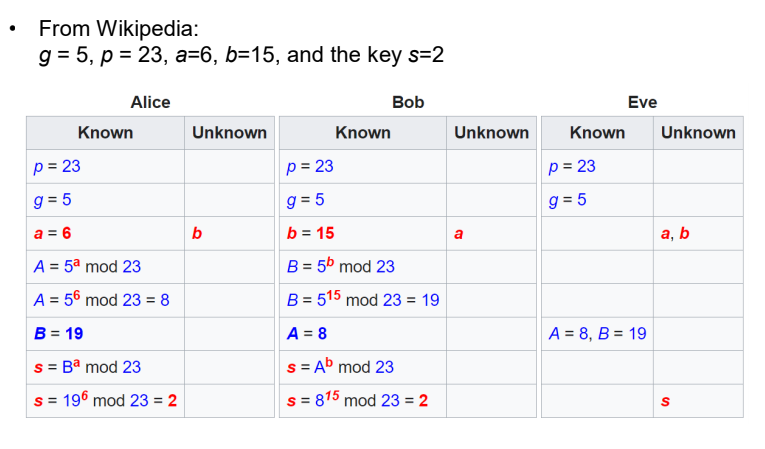
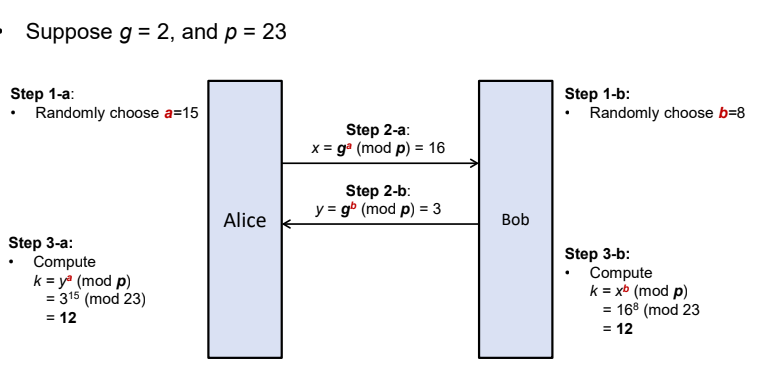
Assunming Bob and Alice have agreed on two publicly known parameters: A generator g and a large prime p

Example

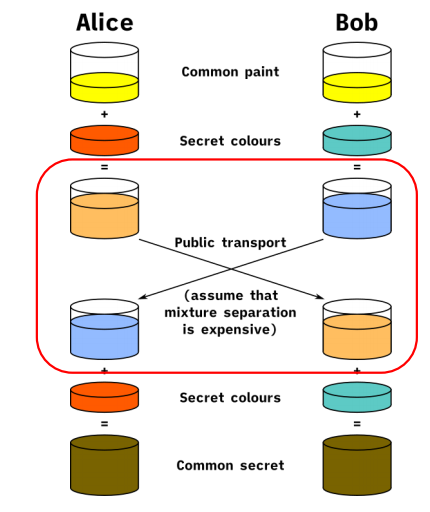
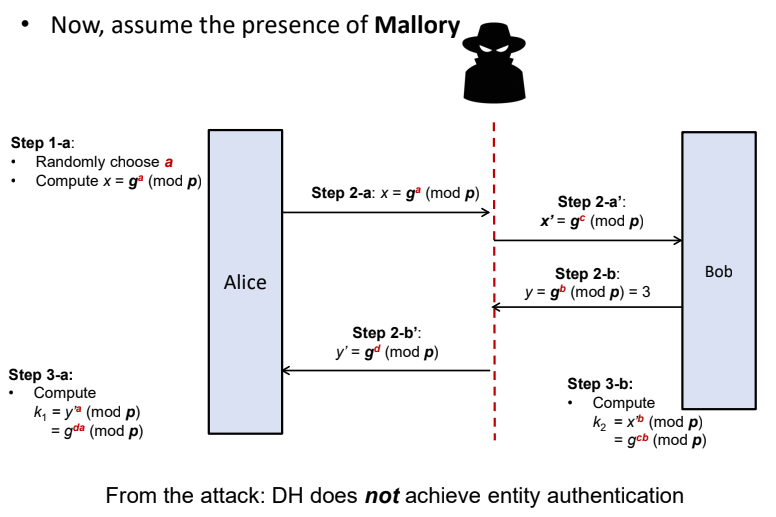
Is Basic/Unauthenticated DH key Exchange secure

• Mallory can just pretend to be Bob to Alice and Alice to Bob
• Mallory becomes MitM

With Mallory:

• Alice mistakes Mallory for Bob
• Since Communication from Alice is encrypted using Ka, Mallory can decrypt it using Ka and renecrypt it using kb
• Mallory can see and modify messsages

PKC based authenticated key exchange cna be easily obtained from existing key exchange

Why

Goals:

• Key secrecy (Confidentiality)
• Entity Authenticity

Solution:

• Incorporate the key exchange process with authentication (Authenticated key exchange (AKE))

Station to station protocol (STS)

• Add signatures to DH: Authenticated key exchange based on DH

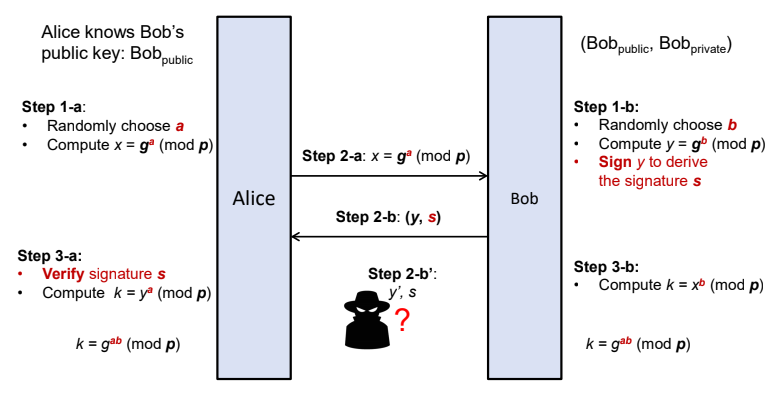
Unilateral authentication: Alice want to authenticate Bob

Mutual Authenticated Key exchange

• Unilateral authentication protocol extended to a mutual authentication: Make alice sign her message in step 2 -a

Requirements:

• Mutual authentication: Alice and Bob must have a way to know public key
• Unilateral authentication: Only one party needs to have a public key
• After the protocol has completed, a set of session keys is establised using a key derivation function (KDF) like HKDF
  • 1 key for encrypt 1 key for MAC
  • Additionally, 1 key for each direction of encryption/MAC

Putting all together: Securing a communication channel

• Communication channel is subjected to sniff and spoof
• A secure channel establised between 2 programs, a data channel that has confidentiality, integrity, authenticity against a computationally bound network attack (Mallory)

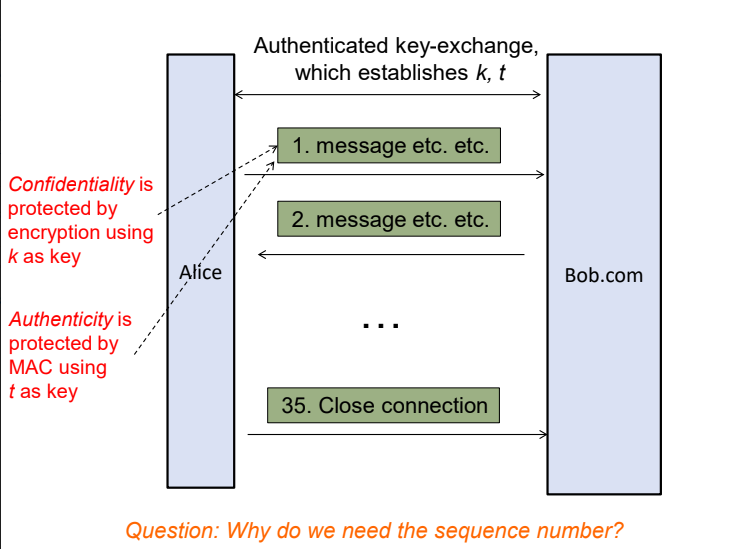
Establish a secure channel between Alice and Bob such that we can protect the authenticity, integrity and confidentialy of the communciation

Secure channel

1. ALice and Bob carry out a unilateral authenticated key exchange using Bob’s private and public key

After authentication both bob and alice known two randomly selected session keys k,t

• k: Secret key of symmetric key encryption(aes)
• t: the secret key of MAC

1. Subsequest communcation between Alice and Bob will be protected by k,t and sequence number i

Suppose m1, m2,m3 are sequences of message exchange, the actual data to be sent for mi will be:

where i is the sequence number, || is concatenation

Secure channel and PKI usage

• Still need distribute public keys
• PKI is use to distribute public key
• Likely involve certificate with the authenticated key exchange

Example:

• Alice visit bob and wants to verify that the entity she is talking to is Bob
• ALice then needs to know Bob.com public key
• Right in the beginnning of the authentication protocol, Bob.com directly sends it certificate which contain his public key to Alice

Putting all together: TLS/SSL

• HTTPs is use to secure
• It is built on top of SSL/TLS:
• Transport layer security (TLS) is a protocol to secure commincation using cyptographic means
• SSL is a predecessor of TLS
• TLS/SSL adopts similar framwork as in the previous part to establish a secure communication channel
• TLS/SSL sits in betweeen TCP transport and app layers

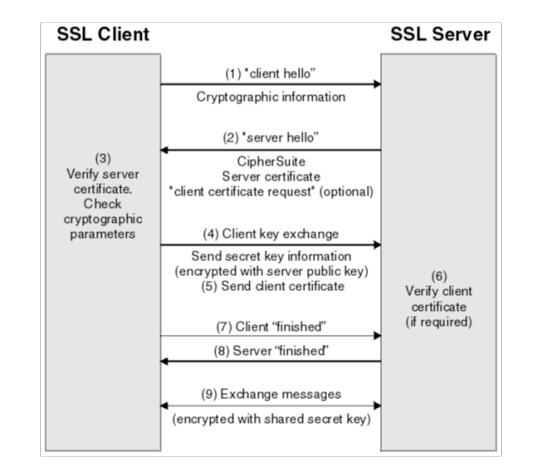
TLS protocol

Tls Handshake

What is a protocol

• A set of rules for exchanging infmation between multiple entities
• A prtocol is often descibe as a set of actions to be carried by entities and data to be transmitted

E.g

Authenticated Encryption

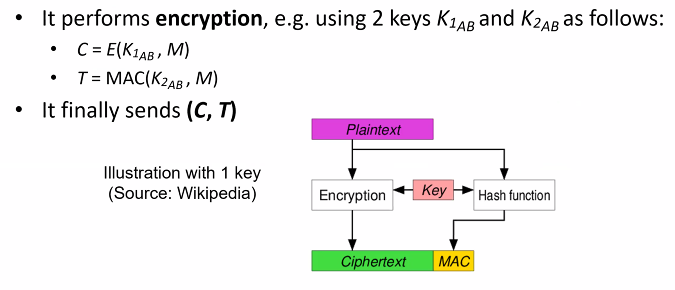
Authenticated encryption is a symmetric encryption that returns both ciphertext and authentication tag

• Combines cipher and MAC: Ensures confidentiality and authenticity
• Authenticated encryption: AE(Kab, M) = (C,T)
• Decryption process: AD(Kab,C,T) = M only if T is valid

Different variants/approaches:

• Encrypt and MAC
• Mac then Encrypt
• Encrypt then mac
• Specialised authenticated cipher

Encrypt and Mac (E&M)

• The sender computes ciphertext C and tag T seperately

• Used in SSH

  Issues: T may not be random looking and could leak info

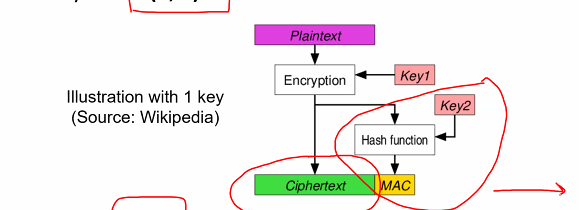
MAC then Encrypt (MtE)

• Sender first compute tag T = MAC(k2AB, M)
• Generates the ciphertext C = E(K1AB, M || T)

• Sends C

• Used in SSL and TLS in ver 1.2

Issue: Decyption is still needed on a corrupted message

Encrypt then MAC (EtM)

• Sender generates ciphertext C = E(K1AB, M)
• Computes tag T = MAC(K2AB, C)

• Sends (C,T)

• USed in IPsec
• Feature: A decryption is not performed on a corrupted message

Authenticated cipher

• returns an authenticated tag together with ciphertext

Birthday attack variant

Birthday attack on hash

• Suppose digest of hash is 80 bits: T = 2^80
• Attacker wants find collision
• Attacker randomly generates 2^41 messages (M=2^41)
• Then M > 1.17 T^0.5
• Hence the prob more than 0.5 among the 2^41 messages, two of them gives the same hash

Variant

• Let S be set of k distict elements where each element is a n bit binary string
• Independently and randomly select m n bit binary string
• Prob that at least one of the randomly chosen string is in S is (larger than):

Notice that the set S and the set of generated m strings are differnet

Other interesting cryptography topics

• Format preserving encryption:
  • Basic cipher cdoes not care if the plaintext is an image
  • Ciphertext is not viewable image
  • A format preserving encryption sovle the issue: - Ciphertext has the same format as the plaintext
  • Other possible target plaintext types: IP address, zip code, credit card numbers
• Fully Homorphic encryption
  • Enables user to replace a cipher text C = E(K, M) with another ciphertext C’ = E(K, F(M)) where F() is a function of M without ever decrypting the initial ciphertext C
  • This is useful for cloud provider: Does not need to know the content of M in order to change
  • However this is very slow

Slides