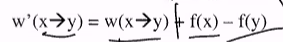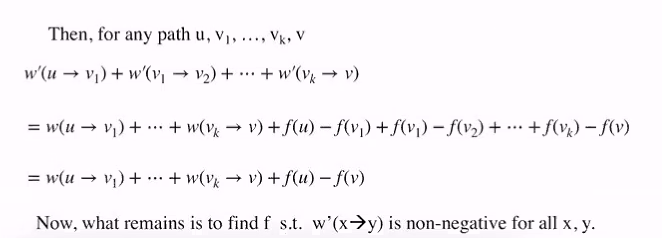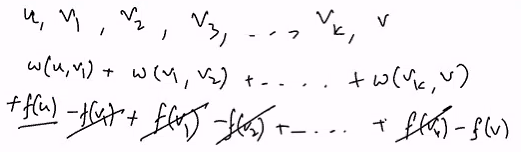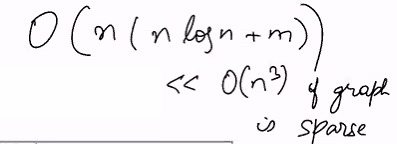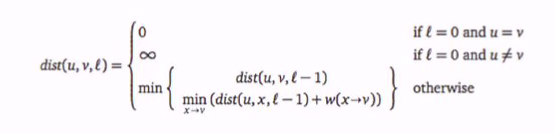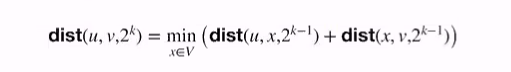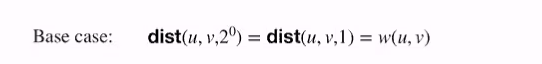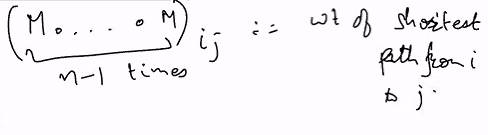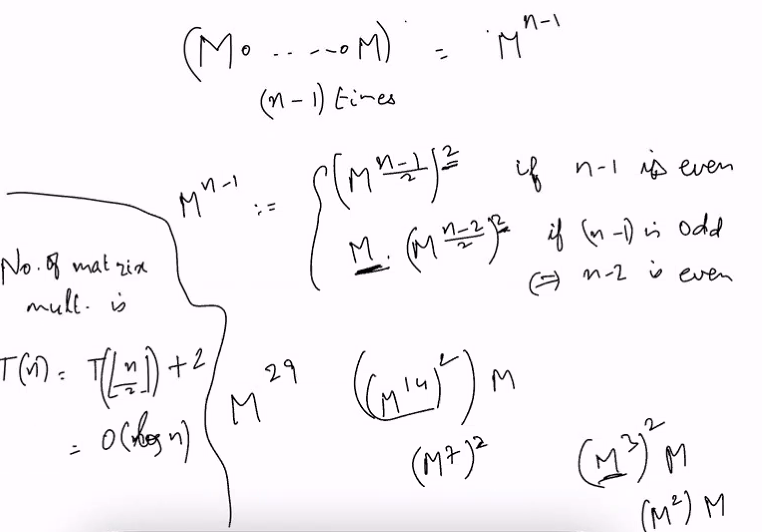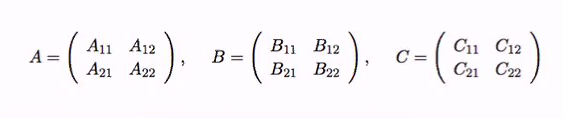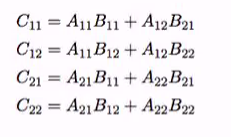All Pair shortest path

Problem: A graph = (V,E), with a weight function w:E-> R. For every u,v in V, find the path of minimum total weight from u to v.

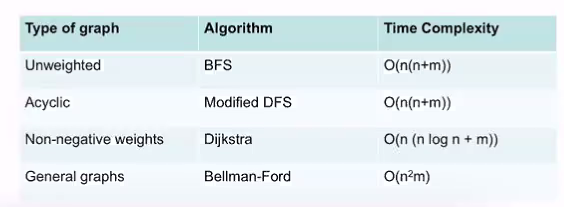
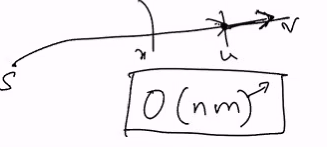
Obvious algorthims: Run single source algo on all v in V

• Acyclic: Does not have cycles

Reweighting

Negative weights means running bellman ford.

• No neg weight : O(n(m+nlgn))
• Neg weight: O(n^2m) = O(n^3)

Negative edges slow us down signifiantly. Can we rid them?

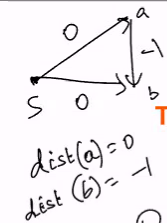
WE cannot add constant because it will change our shortest path due to the possible difference in number of edges (IF we add constant, the weight will change depending on the number of edges)

Johnson idea: We want to reweight the graph in a way that the total weight of any path from s to t changes by the same amount.

Idea:

• Suppose for for function f: V -> R, we change the weight of the edge x->y as follows:

Current weight of e (x->y)

• Such that, for any path, the value is just sum the edges w(k->m)
• for each w’(k->m), substitute with the above formula

• We realised that we are cancelling out the repeats:

• It is not clear whether there exist a function f such that w’(x->y) is not negative for all x and y

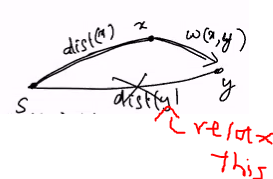
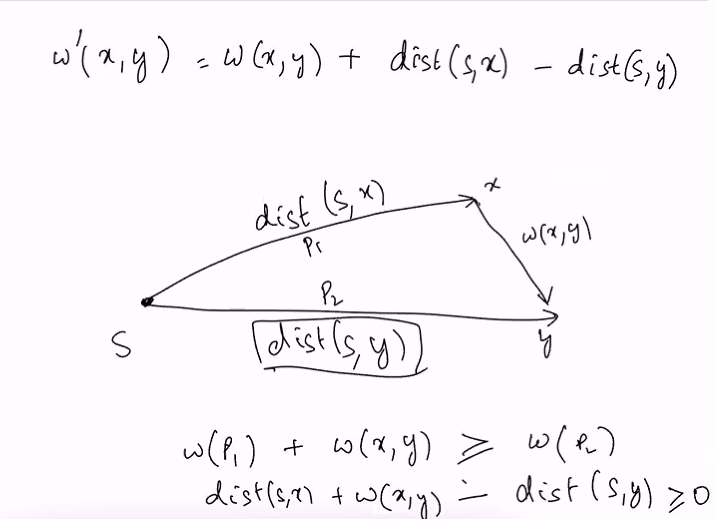
• Notice that f(x) = dist(x), where dist(x) is the distance from some source s satisfies this. (If nt, we shld be able to relax the edge x->y):

• The graph might not have a vertex s from which every vertex is reachable
• we don’t want to subtract infinity

How?

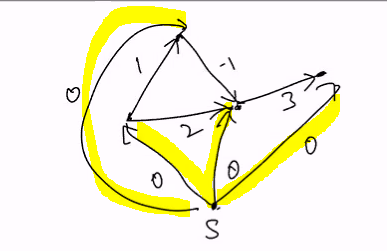
• Add vertex s to graph and add edges s->v to all v in V, with w(s->v)=0

• Every vertex is reachable frm S (We cannot let them use S as a path)
• For any u, v in V, we dont create a new path since there are no incoming edges to s. Thus dist(u,v) remains unchanged.

The function gurantees that the new weight is always not negative and it will not affect the accuracy of the sum of weights (Ie, adding the constant does not change the total sum in relation to each path)

Take note:

Why is it always greater than 0

The value of p2 is always smaller than the sum of p1 + weight. Ths must always hold true that p2 is smaller because if not the sum of p1 + weight will be choosen as the smallest path already

Algo

Time complexity

• One call to bellman ford
• n calls to dijkstra
• Reweighting takes O(m) time
• Total time O(mn + nm + n^2logn + m)

BellMan Ford (Alternative simpler dynamic programming)

• Modify bellman ford
• dist(u,v,i) = shortest distance from u to v via a path with at most i edges

n = number of vertices m = number of edges

There is a source s and there is weight from e to r, d(v,i) is the shortest distance to v that uses at most i edges

We assume the graph does not have negative cycles (0<= i <= n-1)

Variance:

• i : 1 to n
• u: 1 to n
• v: 1 to n
• x: (x,v) is an edge [m times]

Recurrance: d(v,i) = min ( d(v,i-1) , min (d(u,i-1) + w(u->v)), u->v)

Take the previous v and try all of them

	The base case is d(v,o) = inf if v!=s 
							= 0 if v =s

Time complexity is O(n^2m)

Complex: O(n^2m)

Shortest path from u to v is dist(u,v,n)

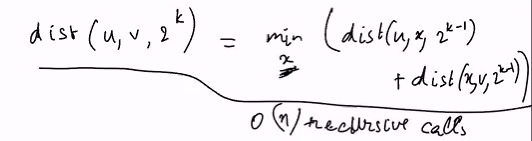
Divide and conqure speed up

Previously, we took x as the closest vertex from the back..

• Speed up by having x as the middle element in the path from u to v.

Variance:

• K: 1 to lgn
• u : 1 to n
• v : 1 to n
• x : 1 to n

We sped up k as logn

Recurrance:

Base:

• k will go from 0, 1,2 all the way to logn
• define another dist*(u,v,k) = dist(u,v,2^k)
• Finding the minimum value of the dist from u to x and x to v
• shortest path by using k = logn (base 2)

Matrix multiplcation

Consider two n*n matrix A and B such that C = AB.

Cij = Ai1B1j + Ai2B2j + .. Ain*Bnj

Now, let M be an n*n edge weight matrix for a graph G = (V,E) i.e.

• Mutliplcation is swap with addition

The value of r = i and c = j of the matrix means the weight for i to j

where 1<= i, j<=n are indices corresponding to the n vertices. Consider the following expressing:

M . M : = min(mil + M1j, Mi2 + M2j, .. Min + Mnj)

Min plus product of matrices

M . M : = min(mi1 + M1j, Mi2 + M2j, .. Min + Mnj)

Reprsents the shortest path from i to j of length at most 2.

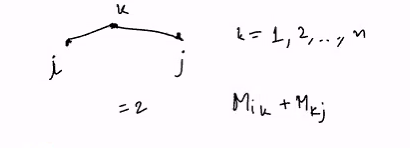
If we take the path from i to j with at most length 2, there will be one immediate index. k = 1..2.. n

Notice:

• Resemblance to the matrix produce MM with
• Multiplcation replace with addition
• Addtion replace by minimum

The weight of the shortest path from i to j is caluclated by the product of all M from i to j (n-1) time

Solving using divide and conquer:

Solving APSP

— Define : MINPLUSPRODUCE(M, n-1) = M. M.M..M n-1 times

For solving APSP notice that it is a sufficient to compute MINPLUSPRODUCE(M, n-1)

Time: O(n^3)

Speeding up

• Let A, B be nn matrices and we want to compute the nn matrix C such that C = AB using divide and conquer.

Notice that: such that

Recursive algo for computing C with 8 multiplcation of M*M matrices where m = ceil(n/2)

Time complexity: T(n) = 8T(n/2) + O(n^2) = O(n^3)

• We have 8 n/2 multiplications
• n^2 additions

If the number is not too large, multiplication does not take much time. In this case, the multiplcations are not matrices which is why it is faster.

Straseen idea - karatsuba style

• 7 magic products
• Each M is n/2 * n/2 matrix products

Improving APSP

• No
• Strassen algo use subtraction - there is unfortunately no similiar inverse for min
• It is an open question whether APSP can be improve to O(n^2.99) It is widely believe that this impossible

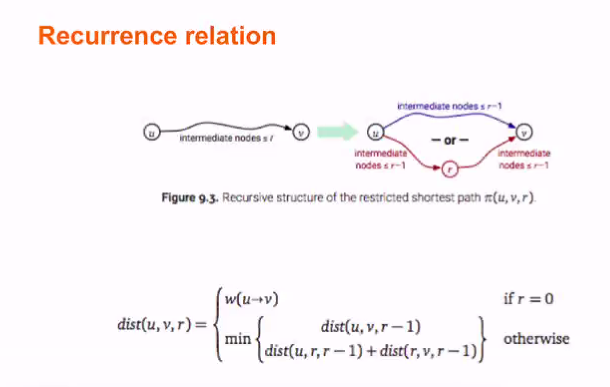
Flyod-Warshall

• Make O(1) recursive call
• Let the vertices in the graph be numberred 1,..n
• We define dist(u,v,r) to be the shortest path from u to v that only goes through vertices numbered 1..r

This dist is not the same as the prev

Recurance relation

• Either use the one 1 to n-1 or use the node r.
• The path using r include the path of 1 to n-1 before choosing r
• We are doing a constant number of recursive calls

Variance:

• n: 1 to n
• u: 1 to n
• r: 1 to n

algo

Slides