Comparison based sorting lower bound

• Suppose we don’t know anything about the content of the input elements we want to sort
• The only reasonable operation we can do to arrange in sorted order is to compare ai and aj for some i and j
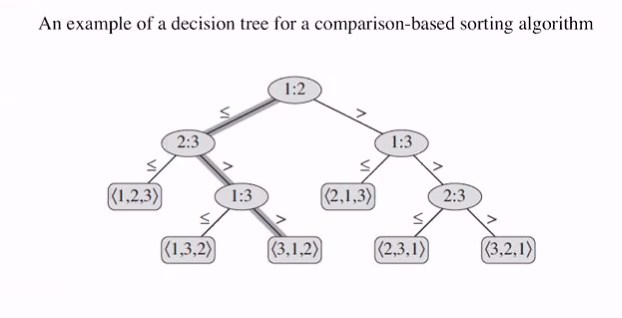
• View any comparison based sorting algo as decision tree

Pictorial:

• Each leaf : Determine specific sorted order
• Worst case complexity is the longest simple path from the root to the leaf

Considering any sorting algo A:

• Let height be decison tree corresponding to algorithm be h
• Number of leaves in tree of height h is N<=2^h
• At each leaves, we must determine which of the n! permutations is the correct order. Thus n! < = N

Combining we get n! < 2^h

Stirling approximation

h = Omega(nlgn) where n!>=(n/2)^n/2

Counting sort

• Sort n numbers {0,1,2,3,4,5…k} where k = O(n)
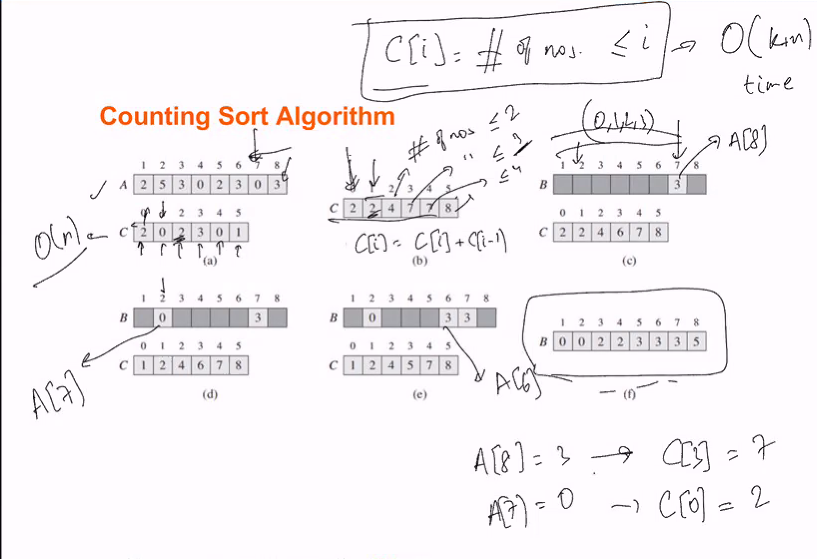
• Maintain array C such that C[i] counts the num of numbers that are less than i and then A[j] is placed in position C[A[j]]+ 1
• Idea might need change if there are duplicate value
• Sorting must be stable too : If two entries have same value then their order shld not change

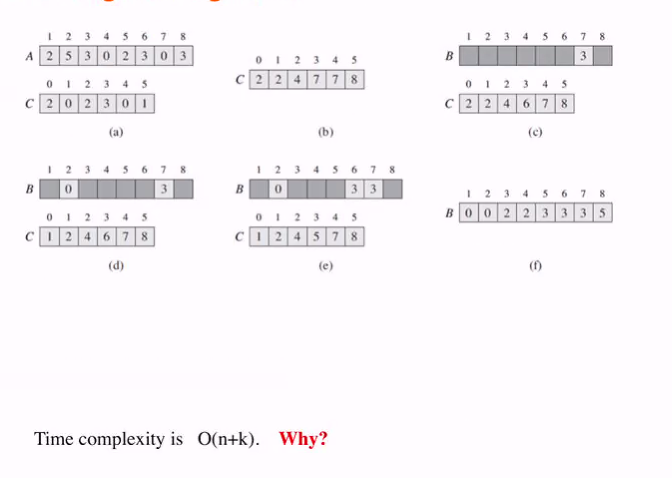
Pictorial:

1. Go through the original array A and store the count of the numbver in array C where the index is the number and the value is the number of times that number is encountered in A
2. Recal C such that each C[i] = C[i] + C[i-1]
3. Fill up B (the sorted array) where C array value is keeping track of the last position of where the value shld be place
   • C[i] = last position where i should be place

Code

• Init B[1..n]
• Let C[0..k] such that C[i] is the number of elements <= i
• For i = n to 1
  • B[C[A[i]]] = A[i]
  • C[A[i]] = C[A[i]] - 1

Time complexity is O(n+k)

Radix sort

• Suppose we want to sort a list of d digit numbers and do it digit by digit
• We intuitively want to sort num based on their most significant bit then recusively sort based on the next sig digit
• But This require maintaining 10 different list of numbers while sorting the 2nd digit, 100 different list while sorting the 3rd digit etc

Radix sort solves the problem of card sorting by counterintuitively by sorting on the least significant bit first

Pictorial:

We are using counting sort to sort each digit where counting sort is stable. This means that we will not change the order of the two numbers if they are equal. Thus radix is able to work.

For d digit numbers, we need d counting sort operations. The only requirement is that the counting sort algorithm is stable

THe algo runs in O(d(n+10) = O(dn)

Given a n in a set of {0..n^2}, - Radix is O(n) - counting is O(n^2) - Merge is O(nlgn)

Remark

One doesnt need to write the numbers in base 10. Sometimes writing the numbers in different base and using radix sort will lead to faster algo

Bucket sort

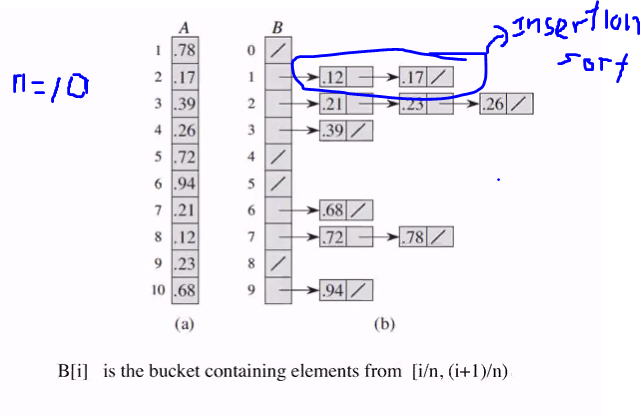
• Suppose we want to sort n numbers drawn randomly from a uniform distribution over an interval. Without loss of generality, let interval be [0,1)
• Create n buckets of equal size [0,1/n) , [1/n, 2/n),...[(n-1)/n,1)
• Since inputs are uniformly distributed over [0,1), we dont expect many numbers to fall into each bucket
• Produce output: Sort the numbers in each bucket and then go through the buckets in order, listing the elements each
• Use insertion sort to sort buckets

Pictorial:

Complexity analysis

• Placing and collecting into different buckets
• Combine them

Slides