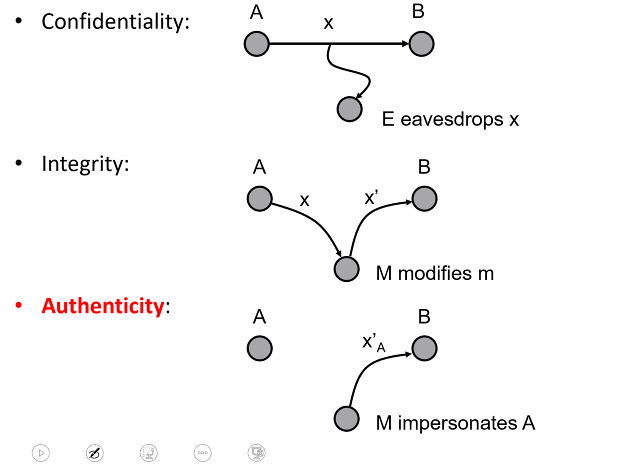
Authentication: The process of assuring that the communicating entity or the origin of piece of infomation is one that it claims to be

Two types:

• Entitiy authentication
  • For connection oriented communication
  • Communicating entity is an entiryt involved in a connection
  • Mechanism: Password, challenge and response, biometrics
• Data origin authentication
  • connectionless communication
  • Communicating entity is the origin of a piece of infomation
  • Data origin authenticity implies data integrity
  • Mechanism: MAC or digital signature

Crypto background: Public key cryptography

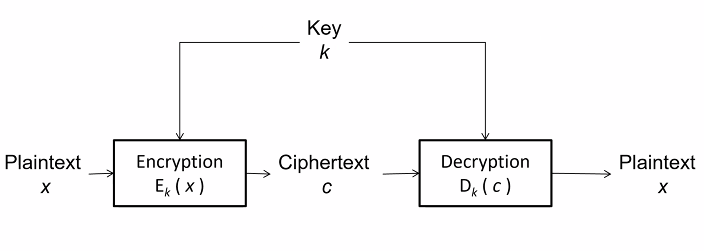
Symmetrical

A symmetrical key encryption scheme use the same key for both encryption and decryption

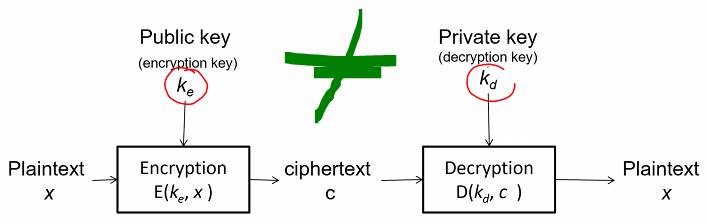
Public key scheme:

A public key (Asymmetric key) scheme uses two different keys for encryption and decryption

• The two key must be related in someway even tho they are not the same

• Typical use: Owner keep private key secret but tells everyone her public key
• Suppose someone has a plaintext x for the owner, the person can encrypt it using the public key and post the cipher text to the owner
• ANother person cannot derive the plaintext without the private key even thou they have the public key

• G - Generates a key pair, publicj and private
• E - Encryption algo
• D - Decryption algo

Requirements:

• Correctness: D(kd, E(ke,m)) = m
• Efficientcy: Fast, polynomial tie
• Security: “one way” function, the E() can be efficiently done but its inverse D() is infeasible without the private key (kd)

Trapdoor function:

• It inverse can be efficiently evaluated with the trap door kd
• Without the kd, there is a asymmetric computational requirenment between E and its inverse D

Security requirement:

• Difficult to determine plaintext without the private kkey
• Implies Difficult to get the private key from the public key

See the tut 4 why cant we require that it must be difficult to get the private key from publick key

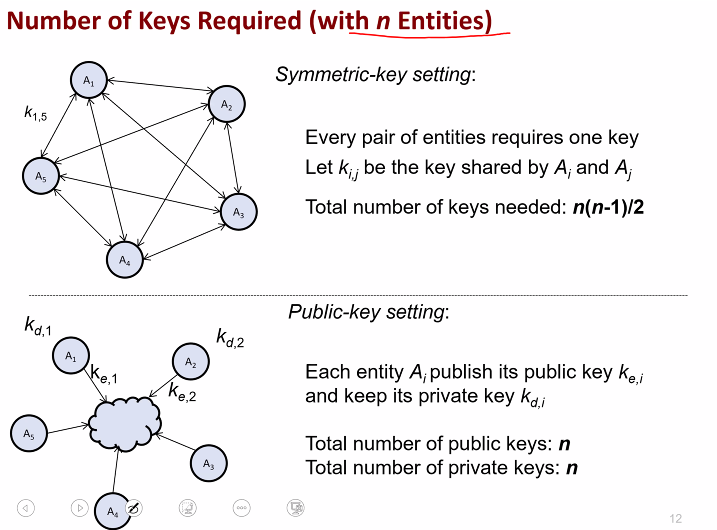
Suppse key scheme and advantages in Key management

• Suppose we have n entities
  • Each of them can compute a pair of public and private key
  • Each announces his public key but keep private key secret
• Suppose A wants to encrypt m for B
  • Use A public key to encrypt m
  • By property of PKC only A can decrypt
• If we use SKC then any two enties must share a secret key
  • Many keys are required expecially if the no of entities is large
  • Establishing all secret key is also difficult

But if we use the public key to encrypt, how do we make it such that someone cant just use the public key to decrypt and get the plaintext? What is the inner working of this such that the attacker needs the secret key since the encrypter only has access to one key (Not the private)

RSA

• Basic form
• Stil requires other stuff like padding
• Integers represented in binary
• When a key is 1024 bits, it means that it can be represented using 1024 bits under binary representation (3 bit int is a value from 0 to 7)

Set up

1. Owner choose 2 large primes p and q and compute n = pq as the public composite modules
   • Note that values of p and q is secret
2. The owen randomly choose a encryption exponent e, s.t gcd(e, fi(n)) = 1 and e is relatively prime to fi(n)
   • fi(n) = (p-1)(q-1) is the euler totient function
3. The owner determins the decryption exponent d where de = 1 (mod fi(n)) ie d = e^-1 (mod fi(n))
   • p and q can throw away
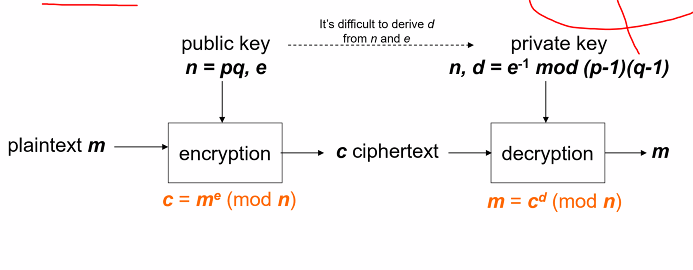
4. The owner publishes (n, e) as her public key and keep (n,d) as private

Encryption and decryption

• Public key: (n,e)
• Private: (n,d)
• Encryption: Given message m, the ciphertext c is c = m^e (mod n)
• Decryption: Given a cipher text c, the plaintext m is m= C^d (mod n)

Correctness

Example

Note

• RSA has a property where we can use the decryption of key d to encrypt and then the encryption key e to decrypt
• This property is not the same in other public key scheme

Algo Efficiently issues:

Security of RSA

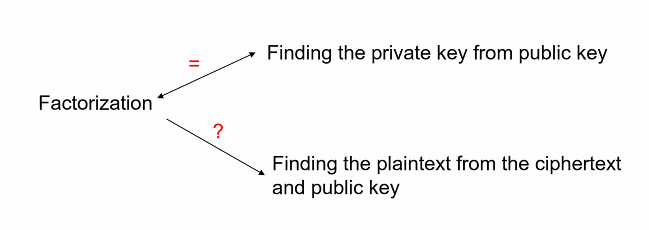
• There is a factorisation problem
• The problem of finding private key from publick key is as difficult as the factorisation.

  We need p and q to derive d

• RSA problem: Finding the plaintext from ciphertext and publick key

700 bit number is no longer safe/

Post Quantum cyptography

• In quantum computer can factosize and perfrom discrete log in polytime
• Both RSA and discrete log based PKC will be broken with quantum computer
• Post quantum cryptogrpahy PKC Schems that are secure agaisnt quantum computer

• Lattice based crypto

• Multivariate crypto

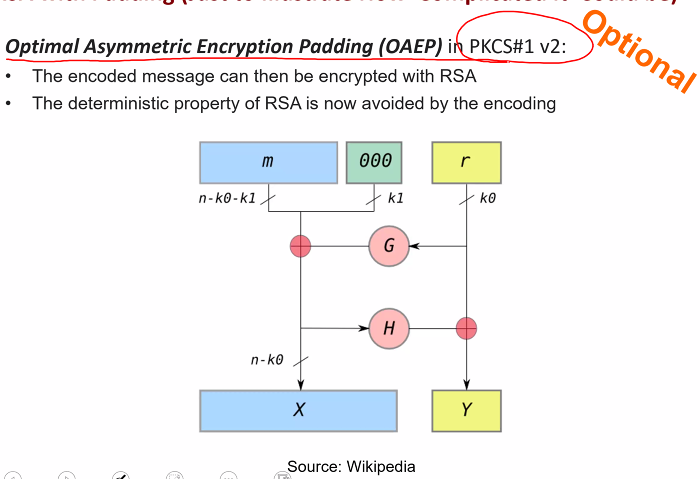
Padding RSA

• IV is required so that encryption is randomised
• Addiitional mechanism must be use
• Homomorphic property

Improper RSA usage

Consider a sample scenario: “ For his final year project, bob is tasked to write an app that employs an end to end encryption to send images from a mobile phone to another mobile phone over wifi. The sender and recipient use SMS to establish the required symmetric key.:

• Bob feels that RSA is cool
• Instead of employing AES, Bob employs RSA as the encryption scheme: The public secret key pair is treated as symmetric key
• Bob claims RSA is more secure than AES, it can be proved to be difficult as factorisation which is believe to be hard
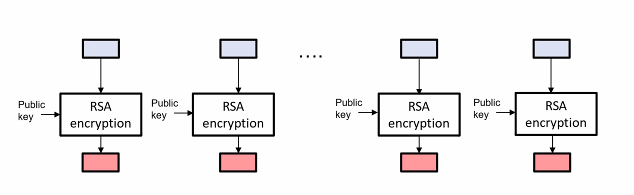
• RSA implementation: To encrypt a large image, bob dividese the files into chunks and apply RSA to each chunk
• Implmentation diagram:

What is wrong?

• Its not true because RSA is still slower, it the seed is long, it will take very long.

Efficiency and performance

• RSA is slower than AES

Solution:

Use AES first (For a large file)

IN practice, it is not commonly known to use RSA to encrypt large files

ECB with RSA

• Dividing the plaintext into piece and independently apply encryption to each of them could leak important info -Suppose the image below is divided into blocks and encrypted with some deterministic encryption scheme using the same key
• SInce it is deterministic, any two plaintext blocks that are exactly the same will be encryption into the same ciphertext

Security of RSA

1)

• Not necessarily more secure than AES
• It can be shown that getting the private key from the publick key is difficulkt as factorisation
• But it is not known whether the prblem of getting the plaintext from the ciphertext and public key

2)

• RSA has to be modified so that different encryptions of the same plaintext lead to different ciphertext

3)

• Factorisation can be done by a quantum computer
  • RSA is broken by quantum computer
  • It is not clear how a quantum computer can be used to break AES

Crypto background 2: Hash and keyed-hash

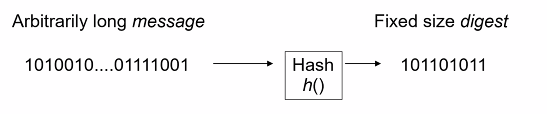
(Unkeyed) Hash

• A function that takes an arbitrarily ling message as input and outputs a fixed size (160 bits) digest
• Note that a hash function takees no key
• A cryptographic has must meet some secuirty requiremetns
• Do not use non cryptographoc has function such as:
  • Taking selected bits from the data
  • CRC checksum

One way - It is easy to get one direction but is hard to go the other way

Examples:

• SHA-1
• SHA-3

Keyed hash

A keyed hash is a function that takes an arb long message and secret key as input and outputs a fixed size, MAC (Message authentication code)

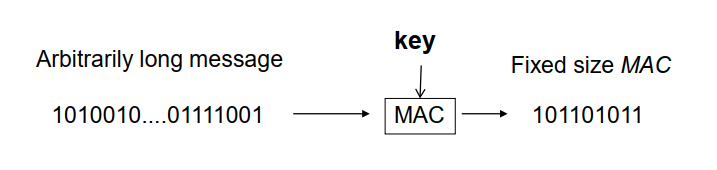
Examples:

• CBC - MAC (Based on AES, A block cipher, under CBC mode)
• HMAC (Hashed based Mac)

Data integrity: Hash without secret key

Example:

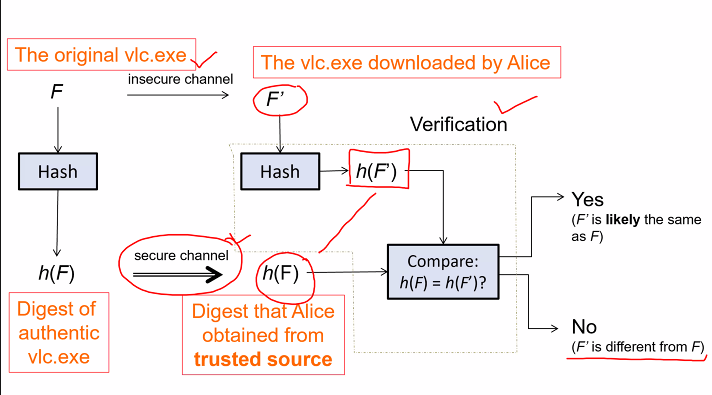
• Someone download a software
• Someone software hosted by 3rd party
• How do we known the autentictiy of the file

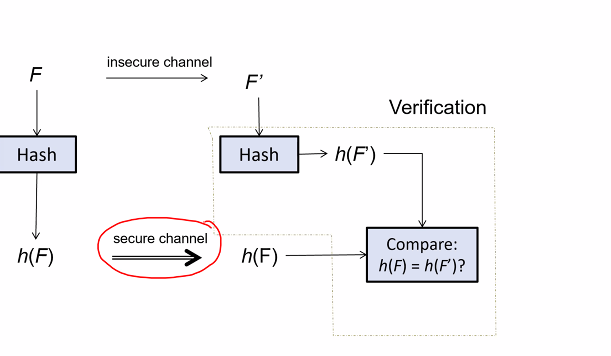
Assuming that there is a secure channel to send a short piece of infomation, the steps are:

1. Let F be original data file
2. Alice obtains digest h(F) from secure channel
3. Alice then obtain a file say F’, whose origin claims the file is F
4. Alice computes and compares the two digests h(F) and h(F’)

Note that even if the hash are the same, does not means that it is 100 percent authentic, just that can say with high confidence it is authentic

• We need the digest to check if its correct

Attacker can find another F’ that givves the same digest

• Integrity is not about authenticity, digest can be forged

Data Authenticity (Mac, signature)

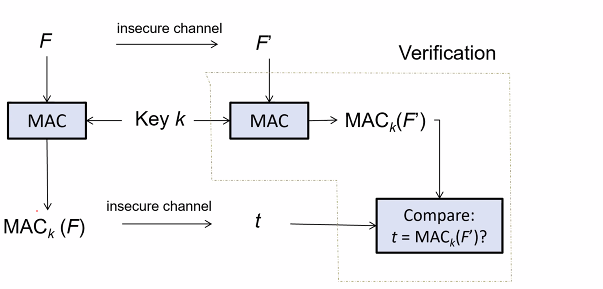
MAC

• MAC might be also modified by attacker

• Typically MAC is appended to F, then they are stored as a single file or transmitted together through a communication channel, hence MAC is also called authentication tag
• If the MAC is the same, means someone knows the key (Could be genuine or bad)

Remarks

• Attacker try forge a valid pair of file and MAC
• No issues with confidentiality

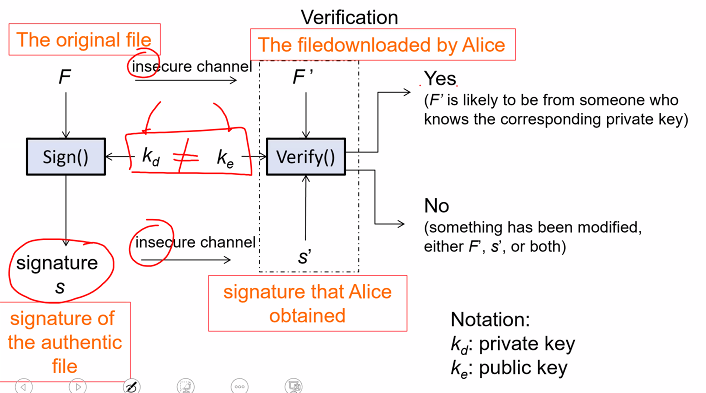
Signature

• Signing the private key is used
• Verification the public key is used

Remarks

• Signature is computed using private key and F
• Computed signature is appended
• Authenticity of F can be verified by anyone who knows the signer public key

What is special about signaure

• We can view digital signature as the counterpart of handwritten signature in legal document
  • Document is authentic or certified if it has the correct handwritten signature
  • No one except the authentic signer can forge the signaure
• In addition to authenticity, signature scheme also achieves non repudiation:
  • Assurance that soemone cannot deny his or her previous commitments or actions

MAC: We cannot force ALICE to admit that the MAC come from her, she can argue that it come from BOB

DIgital signature: It is confirm from ALICE, to generate the signature.. only ALICE can generate it thus it can only be from her

Most signature scheme consist of two components:

• AN unkey hased and sign/verify algo

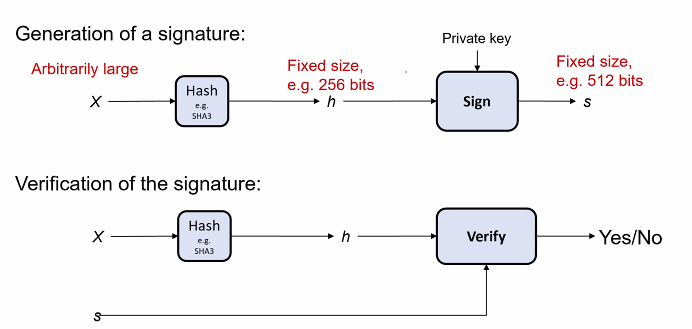
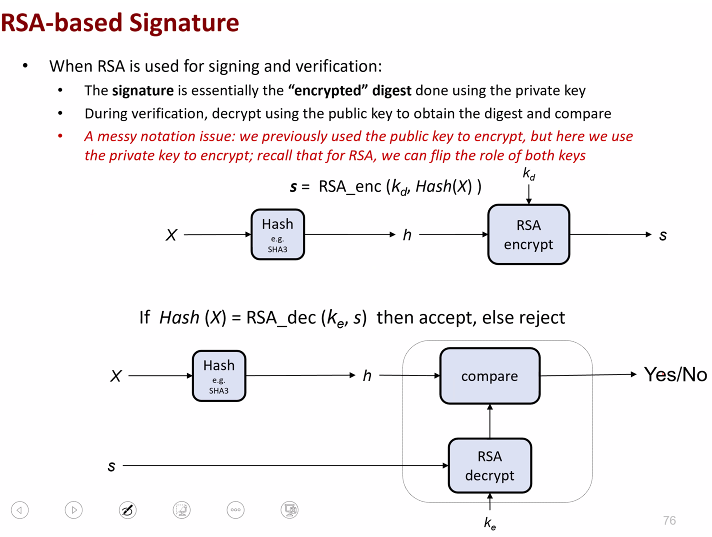
Popular Signature scheme:

• Sign(): Private key encryption
• Verify(): Decryption

Some attacks and pitfalls

Checking the chances: m > 1.17 * T^0.5

• M: Entity
• T: Trait we are comparing

Answer evaluated by 1.17 * T ^ 0.5 is the minimum number of entities for there to be a clash.

Birthday attack on hash

• Hash function are designed to make a collision difficult to find
• Collision involves two different messages that give the same digest
• But all hash function are subjected to birthday attack (Similiar to exhastive search on encryption scheme)

Birthday Paradox

Birthday Paradox (HASH)

• Two messages can have the same tag
• if M>1.17 T^0.5 then with a prob of more than 0.5, there is a pair of messages tagged with the same value

Attack

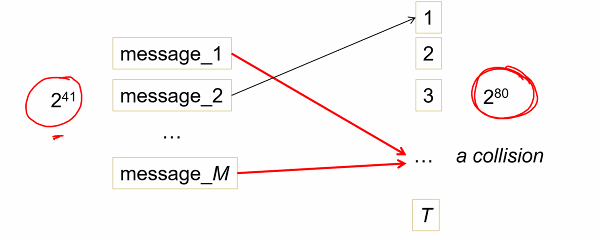
• Suppose the digest of hash is 80 bits: T = ^2^80
• Now attacker want find collision
• If attacker randomly generate 2^41 messages
• Hences with a prob more than 0.5, among the 2^41.. two of them give the same digest

In general the prob that a collision occurs is around 1- exp(-M^2 / (2T))

Implication

• Serious consequences on the digest length required on hash function to be collision resistant
• When key length for a symmetric key is 112, the corresponding recommended length for digest is at least 224
• Why must the digest length be sig larger?

  Birthday attack

Use encryption for authenticity

• Encryption might give a false sense of security
• We should not use encryption for authenticity

E.g:

• Mobile phone and server shared a secret key
• Server can send instructions to the mobile phone via sms
• Suppose the format of isntrcution is: X P
• If an operation doesnt take in paremeter P will be ignored
• There is a total of 16 valid instructions
• An instruction is to be encrupted using AES 256 bits
• It is send as SMS (Which is susceptible to attacks)
• After mobile phone recieves, it decrypts it. If inst is invalid, it ignored else it executes
• Company claim that the communcation is secure: Even if attacker have compromised the based station they are unable to break the security

  What is wrong with this

  • Attackers can span with random instruction and possibily have one of the instruction be the corrct valid instruction

• Encryption is designed to provide confidentiality
• It does not guarentee integrity and authenticity
• A secure design could use MAC instead of encryption

Notes:

• Mac to the instruction is not secure agaisnt replay attacks

Some might argue that encryption is sufficient to protect:

• Attacker doesnt know the plaintext and only knows the cipher
• Change on the ciphertext result in change to plaintext

What an attacker can do to the encrypter message

• Ciphertext blocks reordering
• Integrity attack on one time pad (What happen if 1 bit of the ciphertext get flipped)
  • Modification has a predicatble impact on the plaintext
  • Modification to the ciphertext can be undetected

Because of the bridge of integrity, encryption alone is not enough…

A cipher is malleable if its possible to modify a ciphertext and cause a predictable change to the plaintext

Application of hash: Password file protection

• Password should be hashed and stored in password files
• During authentication, the password entered by the entity is hashed and compared with teh value stored in password file
• It is better to use salt, such that the same password is hashed into two different values for to different userid
• Hashing is two way

Slides