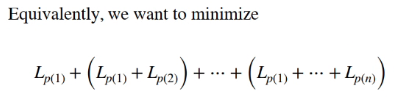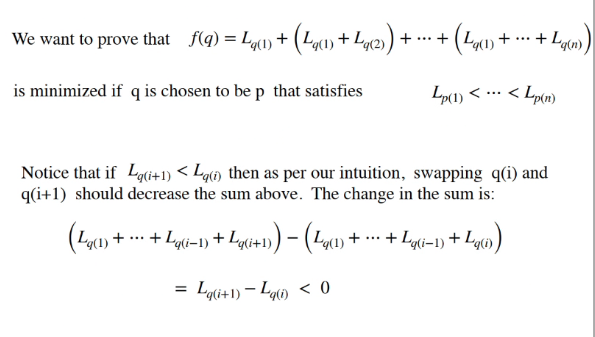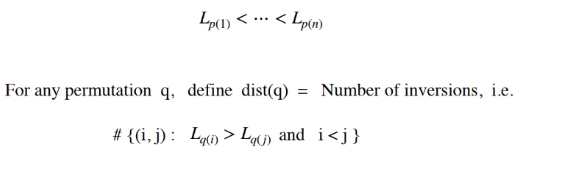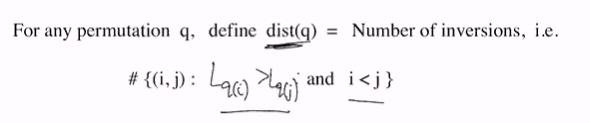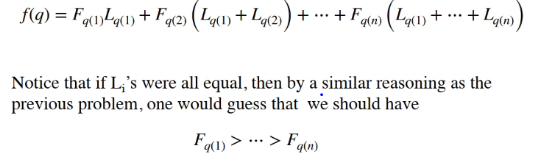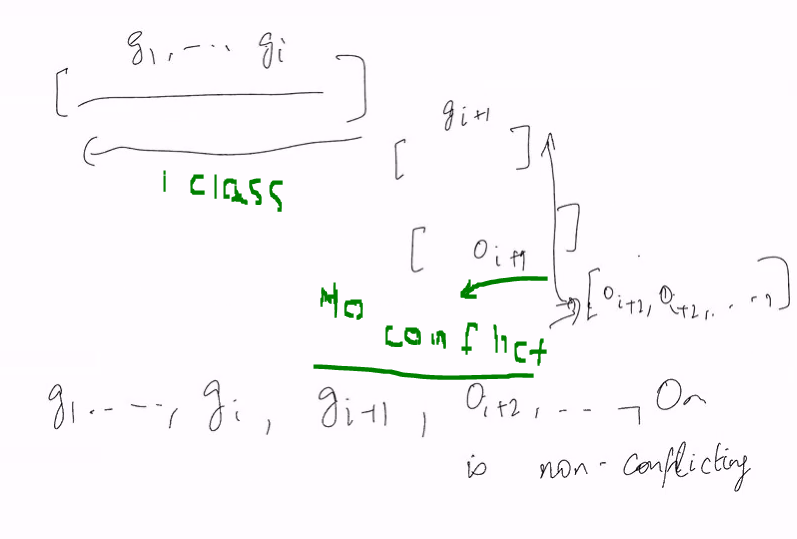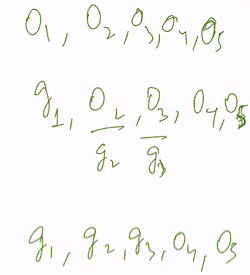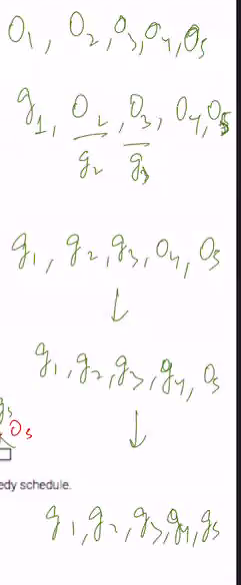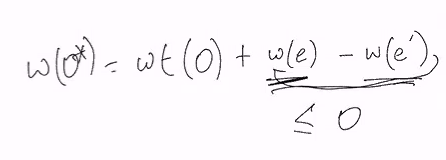Motivation: To figure out which of the option is the best and pick that wihtout making all recursive calls

Storing files on a tape (Minimisation)

• Consider n files we want to store on a magnetic tape
• They have lengths given by L1.. Ln,
• Make a simple assumption that all lengths are distint
• On magnetic tape, reading the kth file requries going through all previous files
• If the files are arranged from 1 to n in the given order then
  • cost(k) = L1 + l2 + l3 … Lk

Problem: Reaarange the files to minimize the avg cost

Theory

• We want to permute the order of the files such that the avg cost of accessing the files are as small as possible.

We want to try to permute

• Back trcking is to costly, there are n! (n^n/2) permutation
• Dynamic programming does not help because we cannot find a small number of subproblems leading to the given problem.
• Guess the solution with initution that Lp(n) > Lp(1)

Our inituition is to pick the smallest

Algorithm

If lets say our guess is correct, then just

• Sort the records in increasing length

We can prove by using local swap/exchange algorithm

Prooving (Local swap for minimisation problem)

• Suppose we are given a problem where we are required to find an optimum solution O where f(O) is minimum
• Suppose greedy algo produce solution G
• We want to prove that for any optimum solution O That minimises f, f(G) = f(O)
• Approach: Slowly change any optimum solution O to eventually get the greedy solution G without increasing f in any step

Steps:

1. Define distance measure (Distance from the greedy solution) dist from any possible solution to a positive number that indicated the distance from greedy solution
   • For any solution S, dist(S) = 0 if and only if S = G: This means that S is the greedy solution
   • dist takes finitely many possible values for any valid solution

Intuitively far from greedy => Far from optimum

1. Given any optimum solution O, different from G, find another solution O* such that
   • Either f(O*) < f(O)
   • or f(O) = f(O) and dist(O) < dist(O)

Our claim is that if our file is increasing order of length then or F(q) is in the minimal order.. so we have to do is to swap some value of p[2] and p[3] such that the value of P[3] is greater than p[2].. note that this would make the order not in increasing anymore

We can see that the difference is smaller than 0 after we do the swap..

Let greedy algo produce a permutation p such that

Observed that dist(q) = 0 if and only if p = q… why?

• Because it is the greedy solution

Collary explaination:

Proving that G is optimal: We want to prove that the greedy is optimal.. if G is not optimal, then there must be another solution that is optimal. Picking O as the optimal solution by minimal distance where O is not G and dist(O) > 0

• O is not optimal (Since O is not G and there exist a O* that is a more optimal solution)
• O does not have the min distance among optimal solution

Therefore the condition where O is the optimal solution by minimal distance cannot hold

Remember f is the function that we want to minimise.

• In this case, our length equation is our f

In this image, let say G is our current greedy solution and lets say O is our optimal greedy solution by minimal distance..

We want to try to get as close to the greedy solution as possible by changing the edges slowly

The goal of distance function is to show that G is optimal:

• if G was the only optimal solution then for any O that is not G, we will find O* such that f(O*) < f(O)
• If there are many optimal solution, then we move closer to the greedy solution G to eventually show that G is optimal.

In this case, we do not need the dist function since LOCAL SWAP gave a solution better than optimal.

Why does this proof work?

Let O be optimum solution such that dist(O) is as small as possible. Since O is different from G, dist(O) > 0

• if F(O*) < f(O), then we have found a solution better than optimum which contradicts
• if f(O) = f(O) and dist(O) < dist(O) then this contradicts that dist(O) is the smallest among all possible optimal solution

Generalisation

Assuming the frequency of accessing file ith is Fi

So if we reorder the files using the permutation q then the cost of the function now becomes:

So intuitvely, we need Li to be in increasing order and Fi to be in decreasing order

• To help figure out the correct greedy choice, we can try a similiar local swap as the prev algo to help us
• Let q* be the permutation obtain by swapping q(i) and q(i+1)

• This consistent with what we expect
• We again make the simplifying assumption that Li/Fi are distinct
• The proof of correctness of this greedy algorithm is almost identical to the prev one. The LOCAL SWAP is already there on the previous slide.

Local swap for maximiation problem

We are given a problem where we are required to find an optimum solution O such that f(O) is max

• Suppose greedy algo produce solution G
• We want to prove that for any optimum solution O That minimises f, f(G) = f(O)
• Approach: Slowly change any optimum solution O to eventually get the greedy solution G without decreasing f in any step

Steps:

1. Define distance measure dist from any possible solution to a positive number that indicated the distance from greedy solution
   • For any solution S, dist(S) = 0 if and only if S = G
   • dist takes finitely many possible values for any valid solution
2. Given any optimum solution O, different from G, find another solution O* such that
   • Either f(O*) > f(O)
   • or f(O) = f(O) and dist(O) < dist(O)

For exam

• Define approporaite dist function
• Convince urself that dist(S) = 0 if and only if S = G and that dist takes only finitely many values (There is no need to prove this)
• Given O, prove that there exists an O* that satisfies the desired property

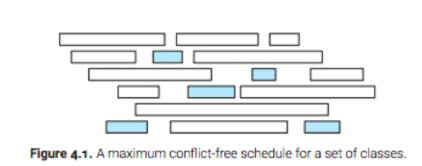
Scheduling Classes

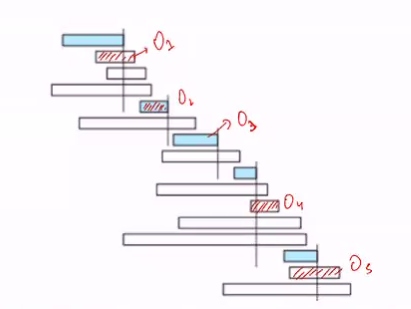
• Suppose you are given two ararys S and F of size n listing the start and finishing times of each class
• Choose the largest possible subset X of 1..n so that for any pair i,j in X.. either S[i] >= F[j] or S[j] >= F[i]

The goal is to schedule as much classes as possible

Naive: Just schedule everything and try everything

Theory

Which is the first class we should pick?

• Think of how to make the first greedy choice
• DO we want to include the class that is the shortest
• Do we want to include class that begin first
• Do we want to include the class that ends first

For each of the strategies above, think of a counter example for which it will not a part of the solution or try to reason why it should be a valid strategy

• If we pick the shortest one, might overlap with another class with the starting time in between the S and F
• IF we pick class that start first, it might go on forever and conflict with every other class
• If pick the class that ends first, seems like it has minimal conflict and scheduling it might be good idea

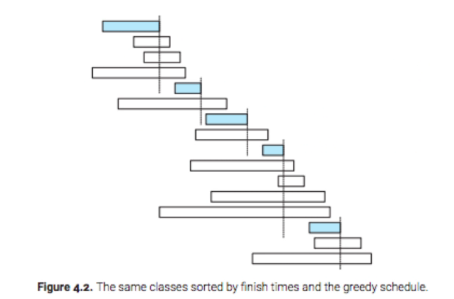
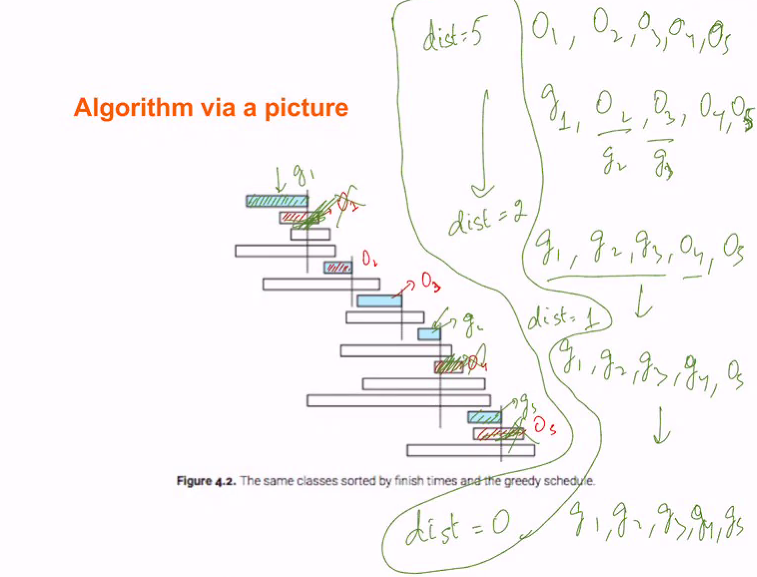
Pick the class that finish first and recurse over all classes that start after this one finishes

• Pick the class
• Remove those that has the conflict
• pick the next optimal one that has no conflict
• repeat

PsueudoCode

• Sort the finishing time of all class from first to last
• Add Class 1 to schedule, Curr = F[1]
• For i =2 to n
  • if S[i] >= Curr, then - Add class i to the schedule
    • Curr = F[i]

Time complexity: O(nlogn) for sort and O(n) for others

Proof

• Suppose optimal schedule O has class {o1..om}, f(O) = m
• Suppose greedy schedule G has classes {g1..gk}, f{G} = k
• We assume that the classes in both are sorted according to finish times
• We want to swap the first class where o differes from G
• Define dist(O) to be m-i where i+1 is the smallest index such that O’i+1’ != g’i+1’

Correctness:

• As long as we are able to keep the same number of classes, then its non conflicting

Since there are multiple greedy solution, we pick the class with the smallest greedy time that does not conflict. We want to show that it is non conflicting:

Prove the number class is the same for my optimal solution and the optimal solution G

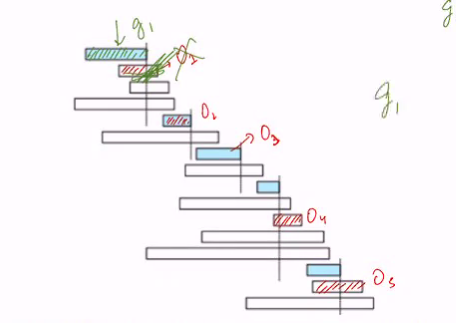
1) You can see the Os are an optimal solution

2) Lets swap O1 with G1

3) When we do the swap we realised that the dist become smaller each swap

swap 1

Swap finish all

Each swap is dist(O) - 1 since our optimal solution would be G where dist(G) = 0

So we can see we will try to decrease dist to be 0

Notice that the number of classes in the origianl optimal is always the same.. it will not increase anymore becasuse we know that the first optimal solution has alr the max amount of classes needed.. thus there is no way the number of classes would increase during the swapping sequence (If it is then the original optimal solution would have already added that class in)

Conclusion

• Try to prove by contradiction
• Prove that the lennma for either local swap (min or max) is correct for the algo we have
• Ensure that the dist is small because if the dist is large it means it is not a optimal solution

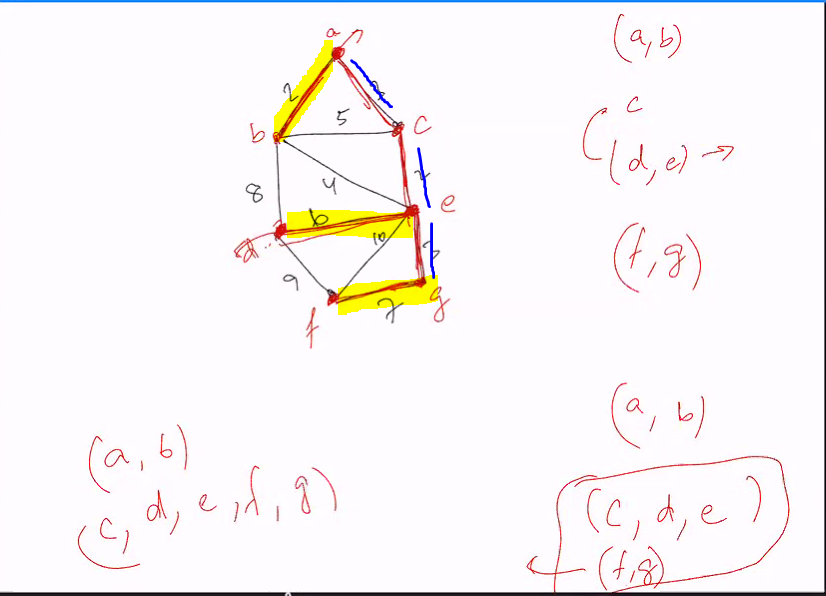
Graphs

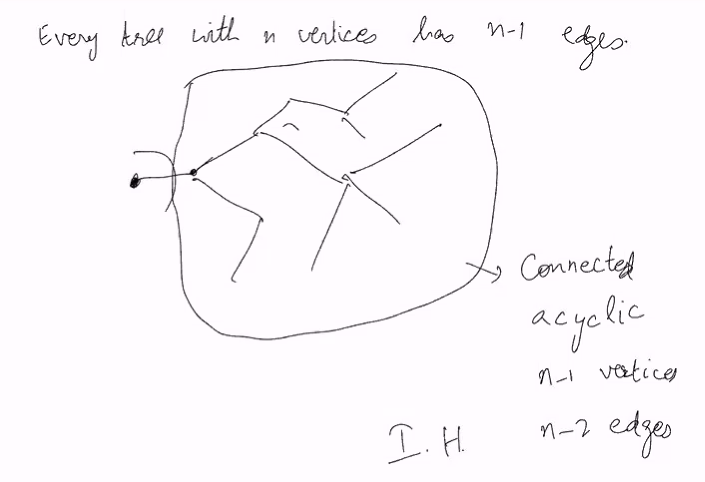
Proof:

1. Every tree has a vertex of degree 1.
2. Each node has at least 2 or 1 neighbours
3. We can loop back
4. We realised that we if we connect back to the previous node, it becoes a cucle

   THis contradicts

Therefore, every Tree has at least 2 vertices of degree 1

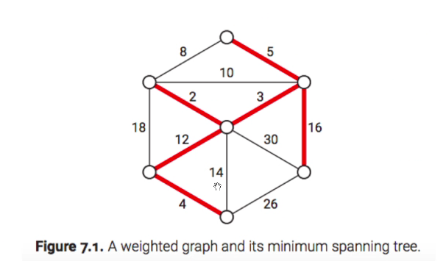
Minimum spanning tree

Onegraph:

• n = number of vertices
• m = number of edges

Weight of the tree is considered to be the sum of the weight of the edges of the smallest weight

Generic greedy algo

It is going to add edges and maintain a forest.

1. Start from an empty edge set
2. Add one edge at a time without creating any cycle

Consider greedy algo for finding an MST of G = (V,E) that finds a spanning tree as follows

• Initilised F = (V,E’) where E’ is empty
• For i = 1 to n-1
  • Let C1 .. Ck be the connected components of F
  • Arbituarily chooe j in {1..k}
  • pick an edge e in E with minimum weight among edges with exactly endpoint in Cj
  • Add e to E’

The main idea is to pick the edge from each component (min) until all is taken

Graph F is a forest

Theory

We assume we have some minimum spanning tree with the same number of edges {o1…on-1}. We can use local

1. Pick smallest index i +1 such that Oi+1 is not ei+1
2. Look at the connected components form by the first i edges
3. add ei+1 to our O (Optimum solution)
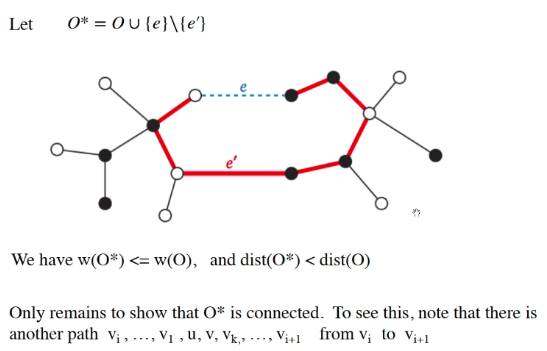
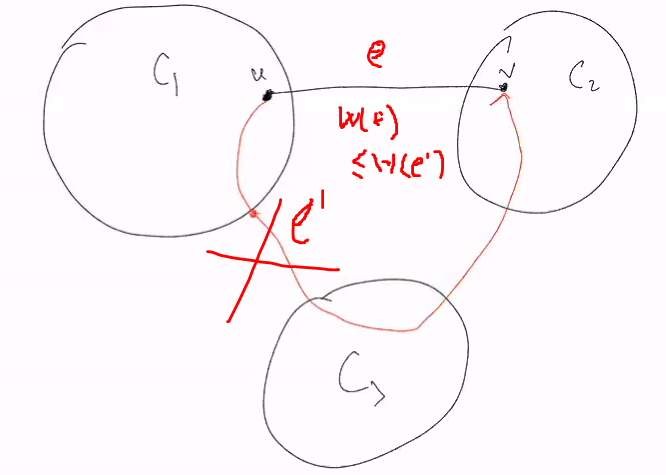
4. In O, where O is the minimum spanning tree, there must be a path from u to v.
5. Look at the first edge e’ that leaves c1
6. Look at the first edge where the vertice is not in c1

The claim is that the swap will either give less weight or be the same but at the same time, have more components then the previous solution.

1. We removed e’ and added e

   Note that we might have disconnected the nodes, but there is another path from the other side

2. Total weight is W(O) + W(e) - W(e’) But notice that

We just need to get it such that for the optimum solution O*:

• W(O*) < = W(O)
• dist(O*) < dist(O)

Check it if the path e is e’

Further explaination

Lets say there is 3 component C1, C2 and C3. There is an edge u to v

We are just replacing e’ with another edge e

• Choose one random vertice
• Check out going edges and select the one with least cost
• Form many components
• Find the outgoing edges one component and see if it can connect to another component
• Choose the smallest edge and merge the two compoennts

• Algo has to choose the edge
• Proof is given the edge

  No matter how you pick the edge, the answer is the same

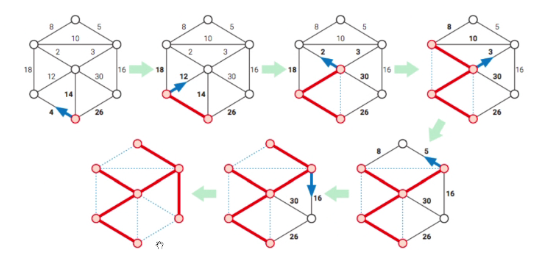
Prims algo

There is only one non trivial component C which is a tree. Every other component contains one vertex.

• Choose one random vertice
• Check out going edges and select the one with least cost
• Check that the connected component is not added
• Add it to our list of components

• Repeat

• See 2040s

Time complexity

• Keep all the edges adjacent to C in a pq Q implemented using a min heap
• At each step, extract the min weight edge (u,v) in Q
  • if both vertices are in tree do nothing
  • If only one, say u, is in the component C then we insert v into C and all edges from v into Q
• Each edge (u,v) can be inserted into Q at most twice.
  • Adding edges from u -　Adding edges from v

• The size of Q is at most M hence insertion/deletion is logm time

• Time complexity O(mLogn) because n^2 is larger than m

Fib heap: O(nlgn + m) time

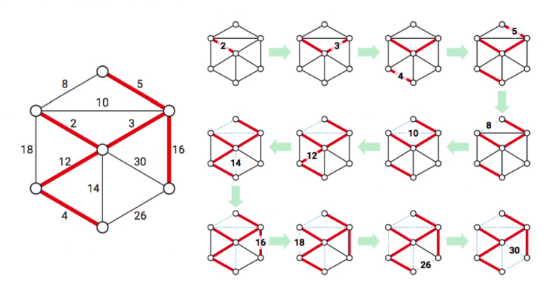
Kruskal algorithm

Scan all edges in increasing order of weight and add the edge if both endpoints are in different components

1. Start with the smallest edge
2. Add the edge into the set
3. Check the next smallest edge
4. Check there is no cycle
5. If no cycle, add the edge
6. Repeat with 3

• Label: Labelling the component (Label is given as the name of the largest component)
  • Every time we merge, we are changing the label of the smaller component to be that of the larger component

Code

Analysis

• After init sort which takes time O(mlogm), the complexity is dominated by teh total time taten UNION operation
• For loop vertex: O(n)
• For loop edge: O(M)
• Each time the component label a vertex changes, the component of F containing the vertex frows by at least the factor of 2, thus each vertex label changes at most O(lgn) times
• It follows the total time spent updating vertex labels is only O(nlgn)

Union is lgn:

• Everytime we merge, we are changing the smaller components with the lkabel of the larger
• The size of this component will be at x2 of the previous
• The next time this component is being merge (And the smaller component value changed to the alrgest) again would be when the component is to be at least x2
• Therefore it would change at most lgn because each time the size of the component will x2

CHanging one component’s label is O(1) but changing all the components in the set is at least Olgn since the larger component would be at most x2 of the previous

2040s:

• Find and union are both logn

SLide