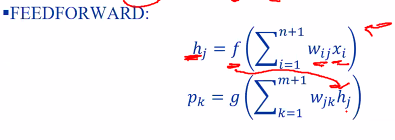Revision: Neural networks

A neural networks contains nodes where the neurons sums the inputs thorough weights. The simplest transfer function (step functioN) will output a 1 if exceed the treshold through an activation function (step function).

• The problem is how to decide the weights
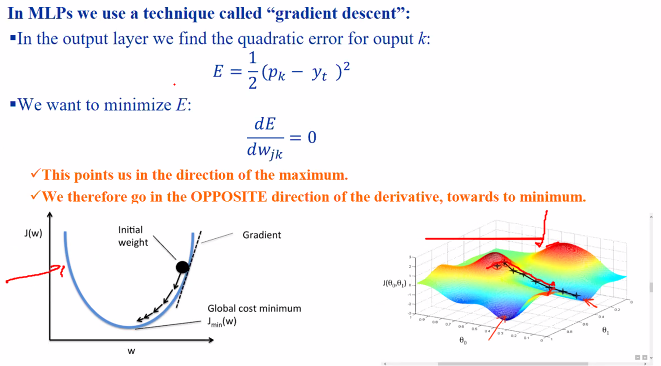
  • we want to find a set of weights that minimise an error function E
  • DE/DW =0 does not means that it is the lowerst point, could be local min

Learning Laws

Unsupervise learning

Throws data and the data will learn by itself by applying its own structure.

• Hebbian learning: Neural networks that strngthen or weaken connections between neurons based on data
• Adversial learning: Two neural networks that comptete with each other based on sample data
• Self organising maps: Partition the vector space based on sample data - “ Clustering”

SOM (Self organising maps)

• Given a sample vector Vk, the neuron that best matches vk accordning to some distance metrics. (BMU)

  We adjust it to look like the input

• Adjust the neighbour except that we adjust it to a lesser degree
• This results in a vector space called “tesellated voronoi surface”

• Run through every neuron
• Find the one that has a smallest distance (BMU)
• Update using the neighbour hood function

KOHONEN SOM ALGO

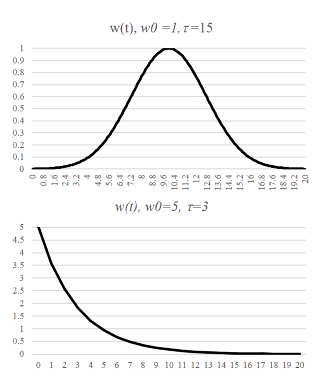
h is known as neighbourhood function

• The BMU will have the maximum value for the neighbourhood function where the change will tbe the greatest.
• As the curve goes further to the left or the right, the change get smaller
• As time passes, our training rate will becomes narrower.
• As time passes, the hat will also become narrower

• The learning rate is similiarly decayed
• The end result:
  • The neurons and their nearest neioghbours are adpated to look like sample data that are closest to them
  • New sample data coming in will auto be classified as the centroid they closest to

KOHONEN SOM auto infers structure from the data presented to it.

Supervise learning

Takes the data and generates the label. Neural will try to mimicks these generated labels

• Data is present in form of (x,y) where x is sample input and y is some kind of target or class that neural networks need to learn

Algo:

• Linear perceptron: Simple, good for classifying linearly separable data
• Multilayer perceptron: Complex, good for classifying non linearly separable data

Perceptrons

Neurons consist:

• Set of Input x
• Set of Weight y
• A unit that does a dot product w^Tx
• An activation fucntion that does the outputs 1 whwen w^Tx + b > 0 and -1 otherwise.

Learning algo:

• Present (xi,yi) to preceptron, where i is a particular sample
• Do a feed forward:
• We take the error (yi-yout) * the learning rate (a)

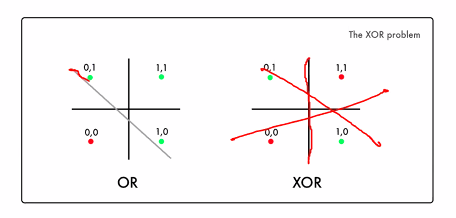
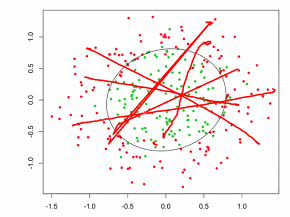
however, perceptrons cannot learn the XOR problem

• No matter how we draw line, we cant seperate the 1 and 0

We want alpha to bring us to the minimum

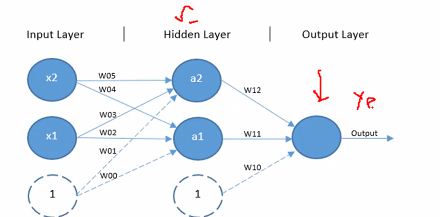
Multilayer preceptons

Consist of:

• Set of input x with n+1 element s(Because of bias)
• Set of n perceptron ndoes called hidden nodes with m+1 terms for bias
• Set of weights connecting x to h
• Set a q perceptron nodes p for the output
• A set of weights wp connecting h to p

Learning steps:

Gradient decend:

• the 1/2 s used to cancel out the 2
• We set the gradient to 0 to find the minima
• This means that the activation fucntion f and g must be differentiable

this could be use to solve our xor problem

Non linearity

Neural network:

• Classification: Classify the input into some label
• regression: Predict xn given x0 to xn-1

Unlike the xor which we can sovle by drawing another line, we cannot do so for every data:

Neura; network Hyper parameters

Weights = Parameters NN = Parameterised models

Neural Network hyper parameters factors:

• Number of input nodes
• Architecture
• Size of each hidden layer
• Number of hidden layer
• Loss function
• Transfer function
• Optimisation function adn their parameters
• dropouts and regulaizer

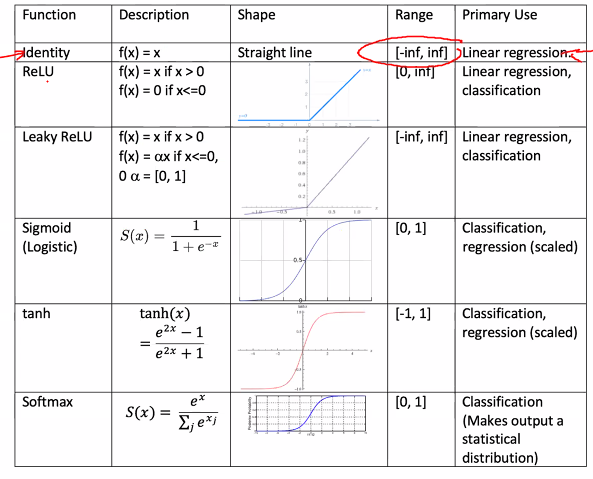
  Activation function

  An activation fucntion transforms the dot products of the weights and inputs.

Uses of activation functions:

• Scaling
• Destroy linearity of output
• Shapuing it to statistcial distribution

Examples:

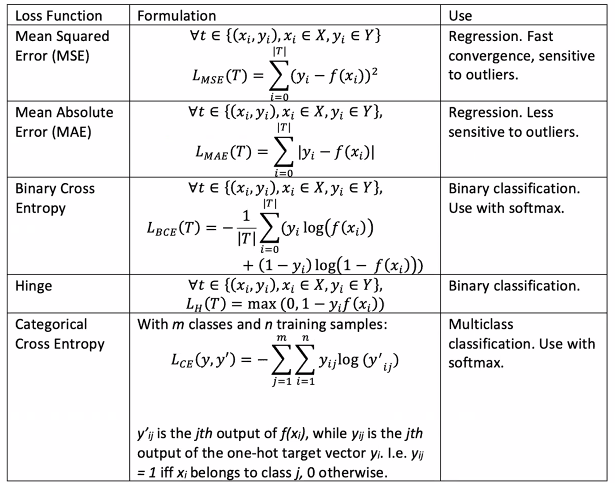
Loss function

A loss function measures the error between function learnt by the NN and the actual target value yi

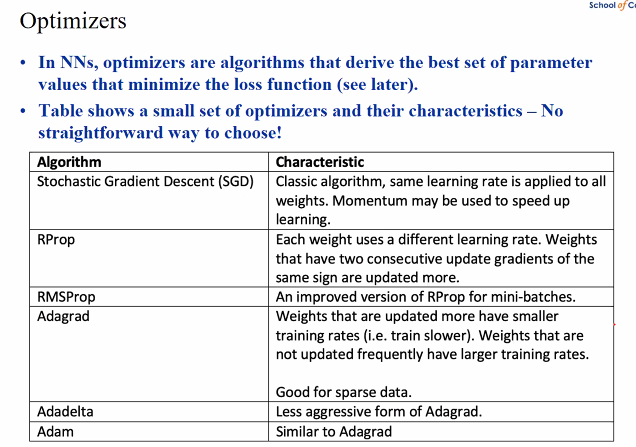
Optimiser

• In NN Optimiser are algo that derive the best set of parameter values that minimise the loss function

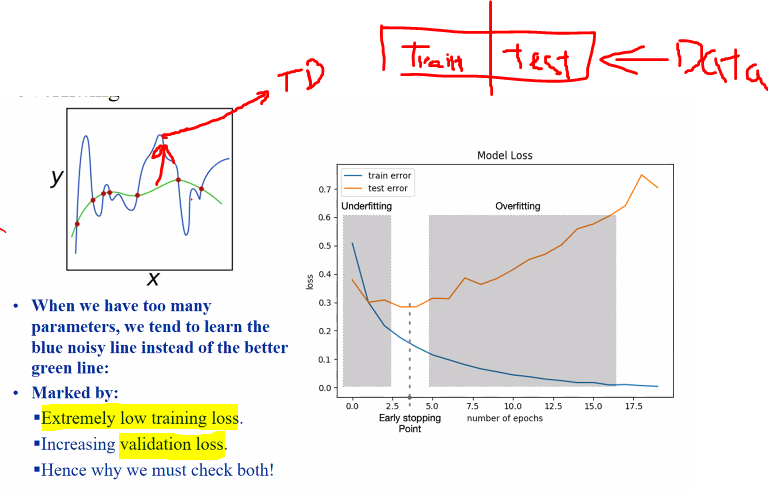
Overfitting

When the model only react well to the training data but not test data.

• Data is Consist of two things
  • Some sort of generator process where the input goes into
  • Noise

Noise is what cause overfitting since noise is very specific to the data fitted in.

We can prevent this by having a simple model with fewer parameters or having more training data

• Blue: training
• Green: Actual data

A good way to fix is to partition the data.

Random noise introduce to the data makes the data looks like other data. (See noise layers)

Slide