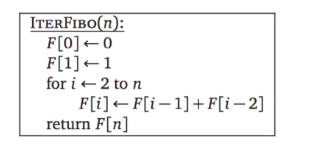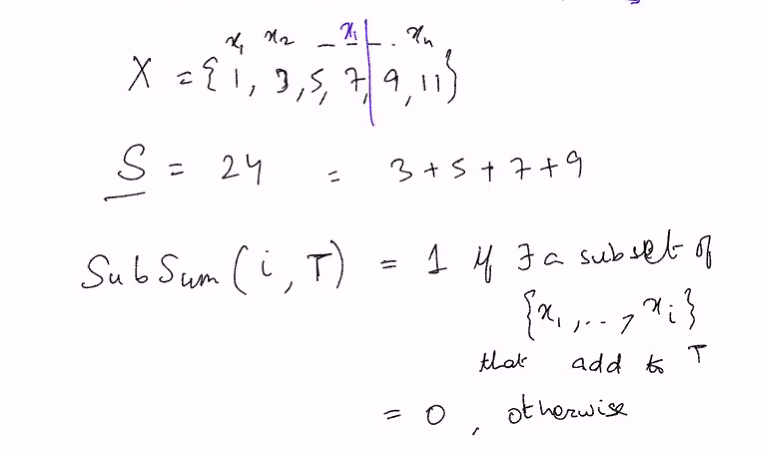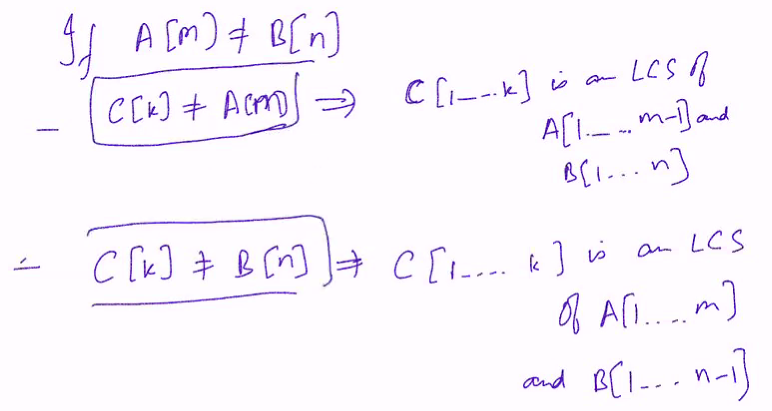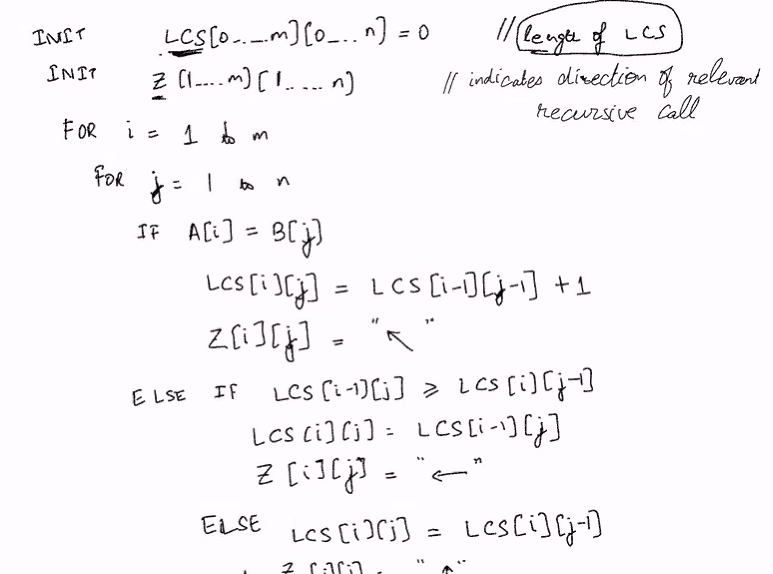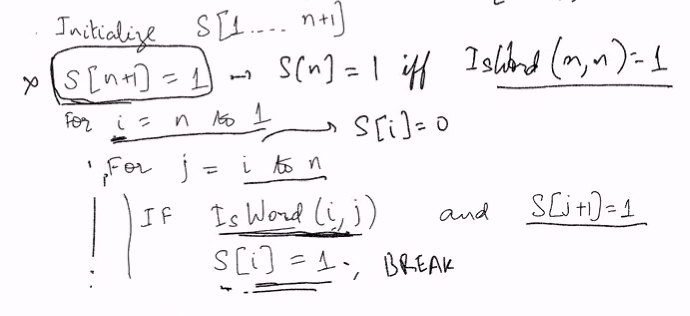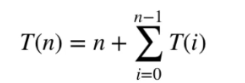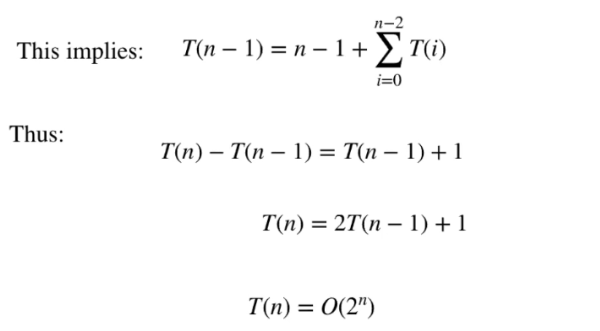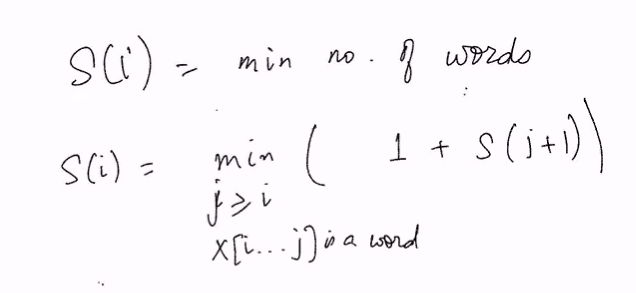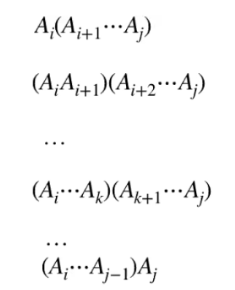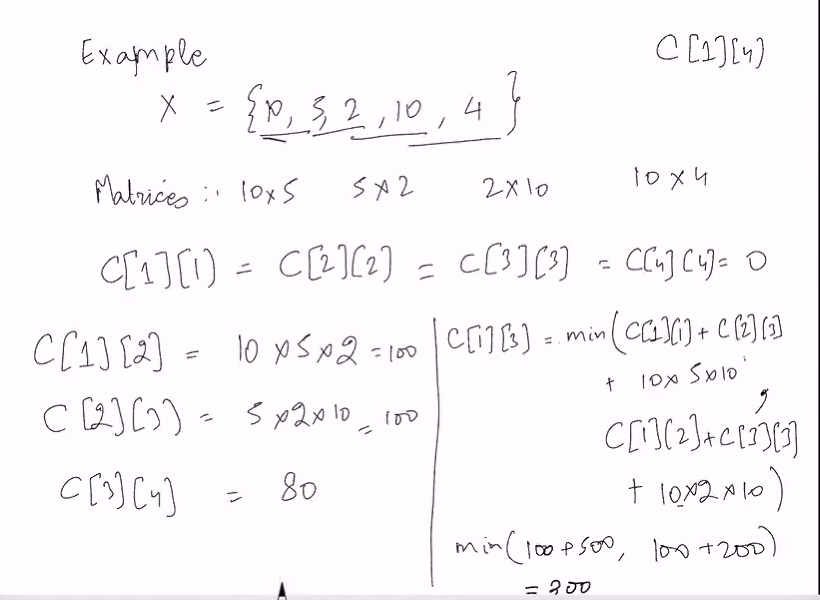Backtracking
- Construct a solution to the problem one piece at a time
- Algo recursively evaluates all alrernatives and chooses the best one
- Algo exp amount of time in the recursion depth
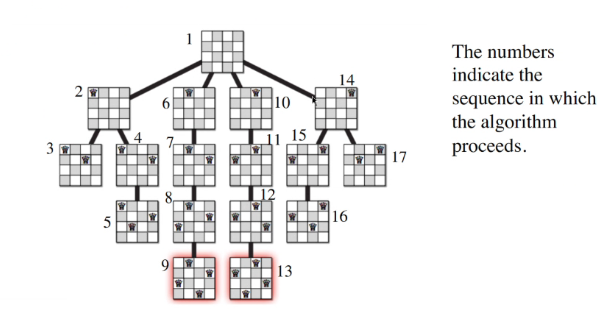
Example: N queens problem
We want to put n queens on n*n chessboard such that no queens are in attacking position (row/column/diagonal)
- For the first layer of the tree, we will only place the queens on the first row
- subsequent children will try to put the next queen on the next row if it is possible
- Else it will backtrack till a possible path is allowed
Looking at the graph stucture, we will see that the order that the configuration are visited is similiar to DFS.
DFS:
- Subproblem = Vertices
- There is an edge from p1 to p2 if p1 makes a recusive call to p2
Algorthims:
Array of Q[1..n] where Q[i] represents the column position of the queen in the ith row
- if i = n + 1, output the value (finish)
- For k = 1 to n (Iterating the col)
- Algo checks if Q[i] = k is valid with respect to Q[1..i-1]: Check if the row and col is valid with respect to the ones we have previously
- if valid, sets and make recursive call with input i + 1 , and Q[1..i] (update)
This explains why numb 3 in the image stops there because the next row cannot be input
Consider the following directed graph for the N queens problem
- The vertices are the states (i, Q[1..i-1]
- There is an edge from (i..Q[1..i+1]) to (i+1..Q[1..i]) if Q[i] is valid with respect to the previous values
One can construct the graph and run DFS on it with the source vertex s being (1, “EMPTY”). If there is a vertex v at distance n, then the problem has a valid solution. One can trace back the path from v to the source s to obtain the solution to the problem.
Backtracking algorthim doesnt build the graph in advance but does it on the fly.
Example: Game tree
Alice and bob play 2 player game
- Alice can move one piece east each step
- Bob can move one piece south each step
- Each player can only move one move at a time or jump one step over the other player
The state is bad when the move player P makes results in the opponents next move state to be good
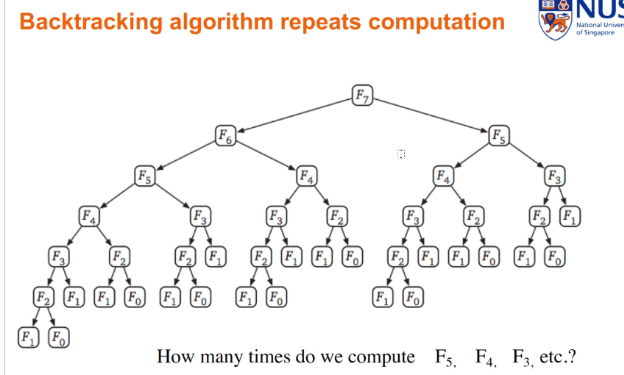
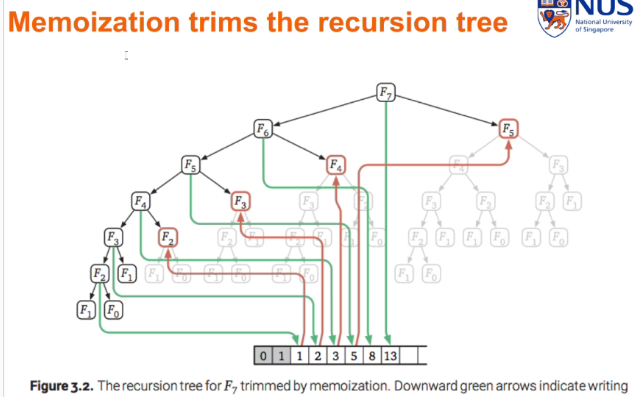
Example: Fibonacchi
- F0 = 0
- F1 = 1
- Fn = Fn-1 + Fn-2 for n>=2
BUT:
SOLUTION:
- Use memorisation
We store the value into an array such that when we need it again, we just have to retreive it from the array. Thus we eliminate the need to recalculate the past.
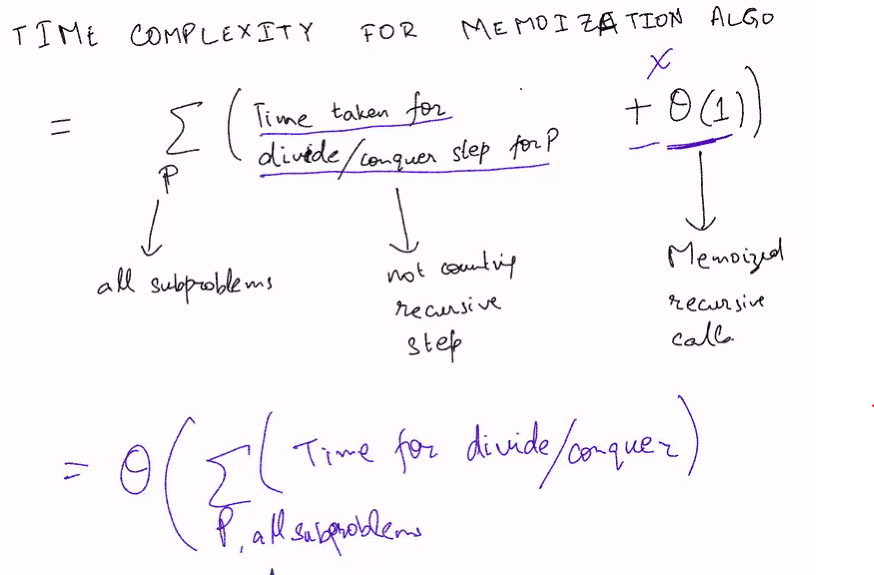
Analyis of algorithm
Recursive algoirthms have 3 steps:
- Divide into subproblems
- Recusively Solve Subproblems
- Combine the solution of the subproblem to solve the larger problem
But the for this algorim, we do not need to recurively solve the subproblem…
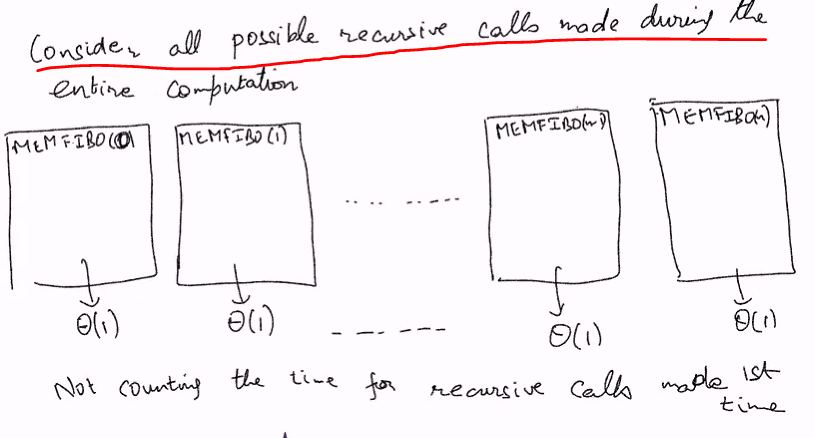
We will classify the recusive calls:
- Memorised recusive calls takes O(1) time
- Recusive calls executed for the first time executes only once > This means that Fib(7) only calculates ones
Consider all possible recusive calls Fn, we know that it will all end up in the base case. Since we do not know which is recusive and which is memorise.. we will just analysis each of the recursive calls not counting the recursive calls that runs for the first time
No time is taken for calling a recusion ie F(n-1)
Proof by induction:
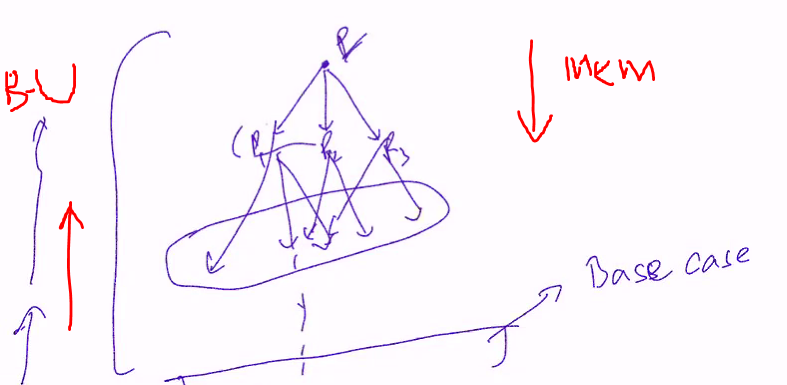
Bottom Up version
Bottom up has the same time complexity for MEMODP up to a constant factor.
Bottom up is similiar to memo except that bottom up start from the leaf rather than the top and does not use recusion
Question: Can all problems if is solvable top down means that it can be solve bottom up vice versa: Yes
Memorisation is DFS
- DFS doesn’t re visit the old paths
- Fibo:
- For every i there is an edge from i to i-1 and from i to i-2
- the vertices are 1..n
- We can construct the graph with source vertex s being n. Before finishing a particulare vertex.. compute the FIB (Fi = Fi-1 +Fi-2)
Compare:
Dynamic Programming
Bottom up and memorisation are both part of DP
Bottom-up
- We can fill up the array iteratvely
Bottom up:
- Many correct orders possible
- Subproblems solve before the probelms
Example: Subset sum
Given a sets of positive integer X and a number S. Determine if there exist a subset of X that sums to S
- If there exist a subset, return TRUE else FALSE
Recurrence
We subtract the number from T each time we did the recusion, this if the last element belong to a valid subset that adds to T.
For each layer, check if the number T gets minus by some X[i] or not, hence the 2 children for each parent
Base case
- SubSUM(X,0,T) = 1 if T = 0 and 0 otherwise
We are trying all possibilities here:
- T < 0 : Output 0
- T = 0 : Output 1
- T > 0 and i = 0 : Output 0, We have exhasted all possible elements
We realised that we can immediately return if
- T = 0 for any i: Return true
- T < 0 for any i return 0
Remark
We can treat X as an global variable so we can decrease the number of parameter
Algorithm
- if T<0, return 0 //SUBTRACTION FAIL
- if T = 0, return 1 // T is exactly X[i]
- if i = 0 and T > 0 , return 0 // T is too big such that there is no values that can be added
- Else return SubSUm(i-1,T) OR SubSum(i-1,T-X[i])
Analysis and remarks
- Correctness: Induction
- Complexity: T(n) = 2T(n-1) + C which solves to O(2^n)
Algorithm with memorisation
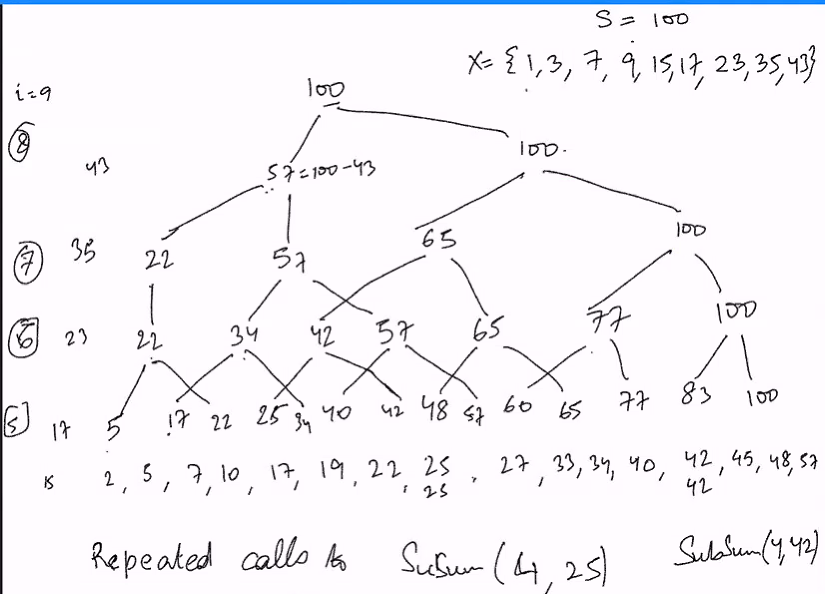
We realised that some of the resultant T is the same in the tree, we could use the memorisation to make this tree faster.
- Initialise array SS[0..n][0..T] all to NULL
SubSum(i,T):
- IF T<0, return 0
- if T = 0, return SS[i][T] = 1
- If i = 0, and T > 0 , then SS[i][T] = 0
- If SS[i][T] is null then
- SS[i][T] = Subsum{i-1, T) OR subSUM(i-1, T-X[i])
- Return SS[i][T]
Analysis and remarks
- The time is O(nS)
- The analysis is the same as the fibonnachi sequence.
It is dynamic programming because we are breaking the larger problem into a smaller problem before solving it
Bottom Up
- Init SS[i][0] to 1
- Try every possible values from T = 1 to S
- If T < X[i]: Then just set the value
- Else: Do the recusive call
In the bottom up algo, we computed some extra values such as SS[0..n][0..S] while in the recusive.. we calculate only the required values. But the time complexity is only slightly different.
Example: Longest Common Subsequence
A string of X is said to be a subsequence of another string if there exist some distint integers such that X[j] = Y[ij] The order matters but it does not have to be continuous.
For example:
- X = “ABSGED”
- Y = “AFERGDW”
The subsequence is “AGD”, Note that the position matters
Recursive solution
Theorem:
- Let C[1..k] be an LCS of A[1..m] and B[1..n]
- If A[m] = B[n], then
- C[k] = A[m] = B[n]
- C[1..k-1] is an LCS of A[1..m-1] and B[1..n-1]
- If A[m] is not equal B[n]
- C[k] != A[m] implies that C[1..k] is an LCS of A[1..m-1] and B[1..n]
- C[k] != B[n] implies that C[1..k] is an LCS of A[1..m] and B[1..n-1]
There are two cases, when A[m] = B[n] and when it is not. If the last character is the same..then it is in the subsequence.
Additionally, if A[m]!=B[n], then clearly we can elimnate the last element from consideration.
Proof
Suppose C[k]!= A[m], in this case.. C[1..k] is a subsequence of A[1.m-1] because the last element is definetely not included into this subsequence. This is similiar situation for B
This proofs the part of the theorem that
- C[k] = A[m] = B[n]
- or C[1..k-1] is an LCS of A[1..m-1] and B[1..n-1]
Suppose that A[m]!=B[n],
The proof here is almost identical to the previous one.
- Proof by contradiction
Algorithm
- Let LCS(i,j) denote LCS (Longest common subsequnce) of A[1..i] and B[1..j] where x\j denote the concat of string x and y
From the previous theorem we get recursive solution for LCS(i,j)
- LCS(i,j) = LCS(i-1, j-1) \ A[j] if A[i] = B[j]
- LCS(i,j) is the longer of the LCS(i, j-1) and LCS(i-1, j) if A[i]!=B[j]
Base case: If any i or j is 0, it means its an empty strings.. so we can return 0
Recurrance:
Do not solve this complicated recurrance but rather use dynamic programming to solve
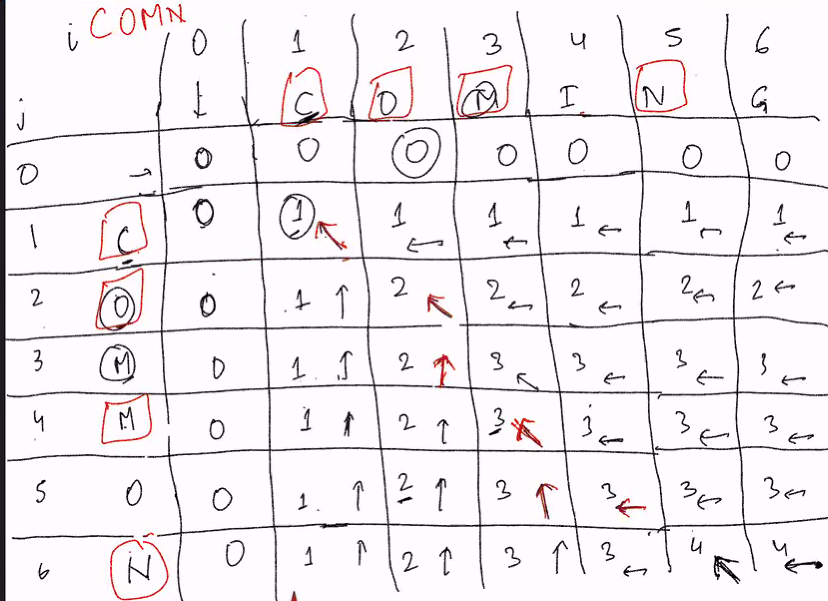
Bottom-up:
We will always have the answer for the previous recusive calls due to the double for loops.
- everytime we see that the characters are equal, we add them together
- Set the current LCS to the greater of the previous answer
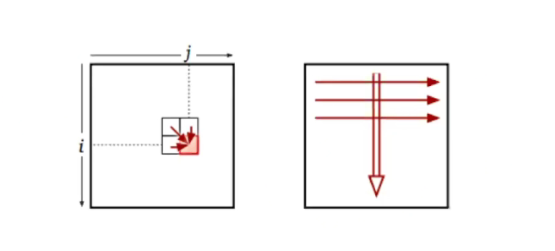
Basically, we imagine the Values to be in a 2x2 matrix where the top row and left column represents one of the strings Each slot of the matrix represents the largest possible subsequence for that letter
The arrow points to which direction the recursion shld go.
Running time: O(nm)
Lecture 4
Memorisation vs Bottom up
| Bottom up DP | Memorisation |
|---|---|
| One should be careful of th3e order in which the array/table is filled | Don’t need worry about order |
| The recursion graph cannot have cycles or the algo will loop forever. | The recursion graph cannot have cycles or else the algo will loop forever |
| Once the order has been correctly determined, the proof of correctness is straightforward from recursion | For a proof of correctness, one must make sure that the recursion graph does not contain cycles and has a bath going to base case |
| The algo might solve sub problems that are not necessary | Algo solve only necessary subproblems |
| Visit the entire recursion graph in reverse topological order | Visit only vertices reachable from start vertex |
| Complexity analysis is straightforward | Need upper bound on total num of entries to be filled. The only upper bound that can be obtatin is the same as DP |
e.g LCS
Bottom up it matters because values might not be computed before the next value happens. For top down, the value will be recursively calculated.
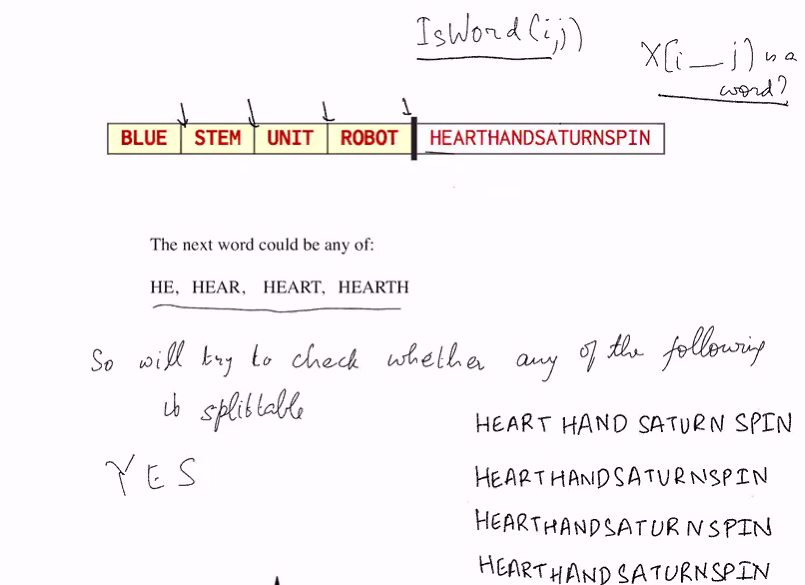
Text segmentation problem
Given a string of text in unknown language without space of punctuation, split this string into its words from a dictionary
- Assume given access to boolean function
isWord(i,j)that returns 1 if X[i..j] is a word
E.g, BLUESTEM return BLUE STEM
BUT
We try everything in dynamic programming and recurse (backtrack)
- Pick first one and make recursive call to the next one
For this question, as long as we get valid splitting
SubString X[i..n], is it splitable?
Recursive solution
- Find function splitable that returns 1 if its splitable
- Splitable(i): Word given can be split into smaller words, 1 if X[i..n] is splitable
- Satisfy recurrance:
Splitable(i) = 1if there exist aj>=isuch thatisWord(i,j) = 1andSplitable(j+1) = 1 - Base case:
splitable(n+1) = 1 - Final one:
splitable(1) - i is the index of the pointer
- j is some random index
- empty string is splitable
Pick the first word, and look at the remaining string:
isWord(i,j) = 1 and Splitable(j+1) = 1
Set it to 0 if not valid and 1 if its a valid splitting
We have to build a solution from n down to 1. Our recursive call that we are making from (i to i + 1, i + 2 … n). For computing S[i], we need S[i+1] .. S[n]
Analysis
T(n) denotes the number of calls to isWord.
Recurance:
This implies:
Time complex: O(2^n) calls to isWord
Backtrack
Splitable(i):
- If i>n: Return 1
- Let B = 0 be a boolean variable
- For j = i to n
- B = B OR (isWord(i,j) AND Splitable(j+1))
- Return B
B = B means that you loop from 0 all the way ip
Analysis:
- T(n) = O(2^n)
Example: Min num of words
- Set S(i) = inf for all i
- If its a word, + 1
- Recursively look at the min numb of words for S(j+1)
Memorisation solution
- Init array
- S[n+1] set to 0 instead of 1
Splitable(i):
- if i = n+1, then S[i] = 0
- if S[i] = init,
- S[i] = 0
- for j = i to n - S[i] = s[i] OR (isWord(i,j) AND Splittable(j+1))
- Return S[i]
Do that for every j and if there exist a j that is a word
Analysis
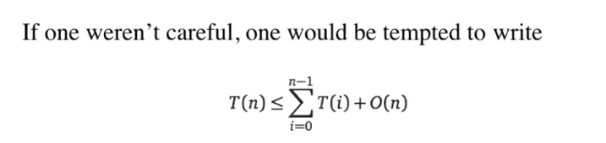
- There are n subprob
- Each subprob makes at most n additional calls to IsWord (Not coutning the calls from its subpron)
- Calls: O(n^2)
Call to S[i] is at most n * subproblem (n)
Time complex: O(n^2) calls to isWord
We are only calculating for the subproblem S[i] so we ask if X[i..n] is splitable. We dont need to iterate from 1 to n
Smallest Edit Distance
- Def: Edit distance is the smallest number of letter insertion, letter deletions or letter substituition required to convert X to Y
- Give two string X and Y, we want to find the edit distance between the strings
- Moves:
- remove chara
- Add chara
- Substitute To solve edit distance:
- Focus on last col
- Try all possibilities
- Remember: DP = Smarter brute force
For example: AL GOR I THM -> AL TRUISTIC would take 6
- Remove G
- Sub O,H, M
- Insert U, S
Recursive
Let Edit(i,j) be the edit distance between X[1..i] and Y[1..j]
- Consider any sequence of min num of insertion/del/sub (IDS) steps
- Conclude that operation done left to right
- Theory: If there exist a sequence of min num of IDS steps that results in modifying string X[1..i] to Y such that in the last steps,
- X[i] is deleted, the
Edit(i,j) = Edit(i-1,j) + 1 - Y[i] is inserted, the
Edit(i,j) = Edit(i,j-1) + 1 - Neither X[i] is deleted nor Y[j] is inserted then
- if
X[i] = Y[j]thenedit(i,j) = edit(i-1,j-1)- if X[i] != Y[j] then
edit(i,j) = edit(i-1,j-1) + 1
- if X[i] != Y[j] then
- X[i] is deleted, the
- 1 is an insertion / deletion Z(i,j) means substituition is required
We dont know what the last step of an optimal sequence is but we can get the reccurance by trying all the option
Bottom up
- Dependenecies: Each entry Edit[i,j], we need Edit[i-1,j], Edit[i,j-1] and Edit[i-1.j-1]
- Eval: Increasing i, increasing j (Other order also work for example increasng i+j)
ALGORTHIM
Compare the 3 and take the minimum
Complexity: O(mn) => the num entries we need compute
Matrix chain multiplication
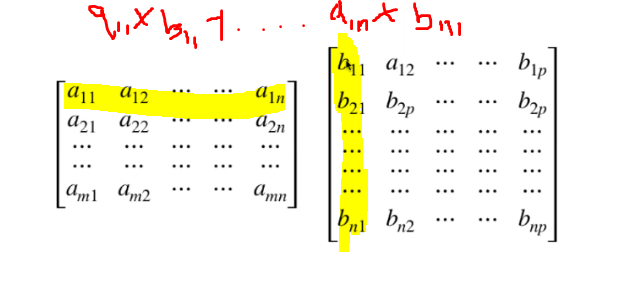
- Multiplying mn matric with an np mtrix to get an m*p matrix
- Requires n multiplication for computing each entry
- Total of mnp multiplications
- Given sequence of n+1 numbers as input X where the ith matrix has dimensions X[i-1]*X[i] for i = 1 to n
- Find optimal parathesization fo the matrixes
Solve the simpler problem of finding min number of multiplcation requried
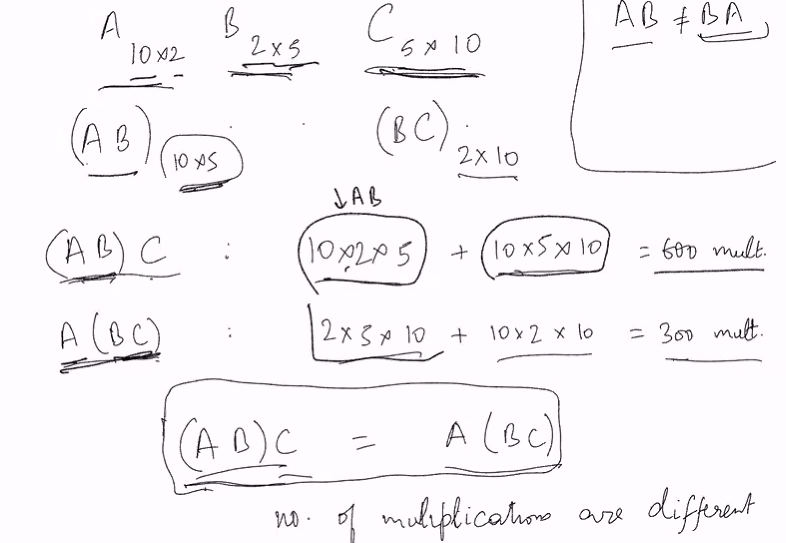
Consider a sequence of matrix:
- A: 10*2
- B: 2*20
- C: 20*5
Then (AB)C is a computatuion that requires 10 * 2 * 20 + 10 * 20 * 5 = 1400 multiplication
A(BC) requires 1025 + 2205 = 600 multiplications
If you multiply at certain timing, can get diff num of multiplcation
Trying out all possibilities:
- Calculate the smallest cost for each time
Given a sequence of n+1 numbers as input X[0..n+1] where the ith matrix has dimesnsion X[i-1] * X[i] for i = 1 to n, find an optimal paranthesization of the matrices
We will solve a simpler problem of finding the min number of multiplication required
Recursive
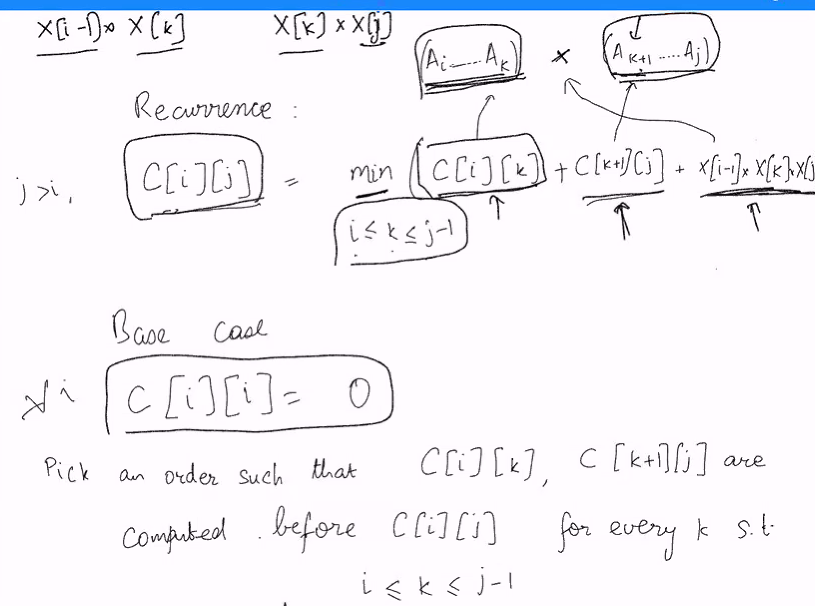
- Let C(i,j) be min num of multiplcation for an optimal paranthesisation of Ai, Ai+1… Aj
- What is the cost of these partitons?
To obtain the recursive algo, consider how the chain can be parathesize
- Look at where we place the first para
- Partition into two parts and compute each parathensis recursively
Goal is to find a recurrance
Bottom up
Base Case: C[i][j] = 0
- We can consider length as
- j - i > k - i
- j - i > j-(k+1)
- C[i][k] and C[k+1][j] should be completed before c[i][j]
- i <= k <= j-1
- Note that increasing i and j does not work thus we can go with increasing length
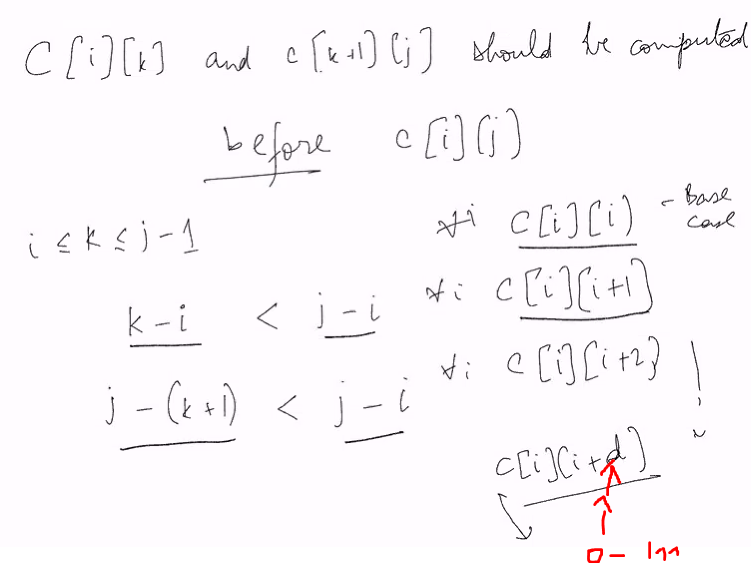
Time complexity: O(n^3)
Split the matrix into smaller parts and solve for those
E.g
Self - study
Memorisation:
- Draw a 2x2 matrix where the x and y col boxes each denotes the each matrix
- Each box in the matrix denotes the num of multiplication needed for muliplying those 2
- Let length denote the number of matrixes used to multiply
- Fill up the matrix starting from
- When length = 1, multiplication is 0
- When len = 2 , we consider a multiplcation of 2 matrix, in the mem array, calculate values for 2 array and store in mem arry
- When len = 3, make use of the previous calculation of matrix (len = 2) and multiply the valus for that matrix. Then sum up the number of multiplcation for the resulting matrixs and store into mem array
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| 0 | 0 | ||
| 1 | 0 | ||
| 2 | 0 | ||
| 3 | 0 |
- For this matrix example where M denotes the array as shown above, A[0][3] means that the matrix multiplcation in order of 0 * 1 * 2 * 3, where each number represents a certain matrix
- After filling up , the answer would be at A[1][n-1], where n is the max value
- Track back
- For a value in A[0][3], means that the multiplcation is(0..2)(3)
- Backtrack to A[0][2] and so on and so forth
Greedy algo
- make the choice locally without having to solve the subproblem
- Looks at one branch of the recursion tree