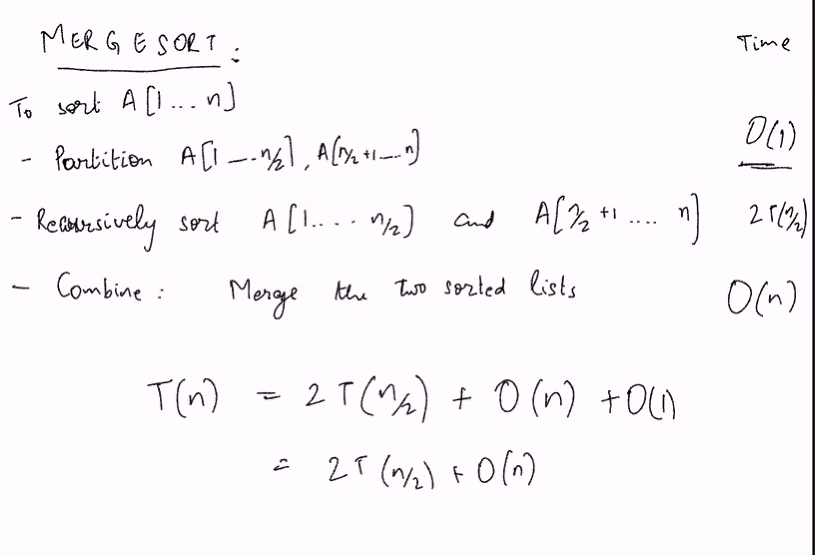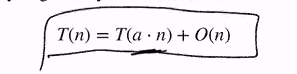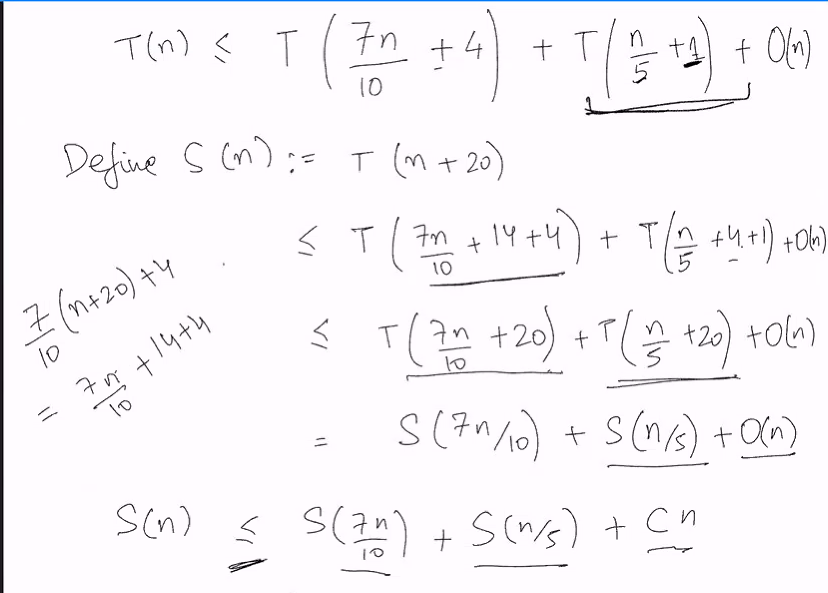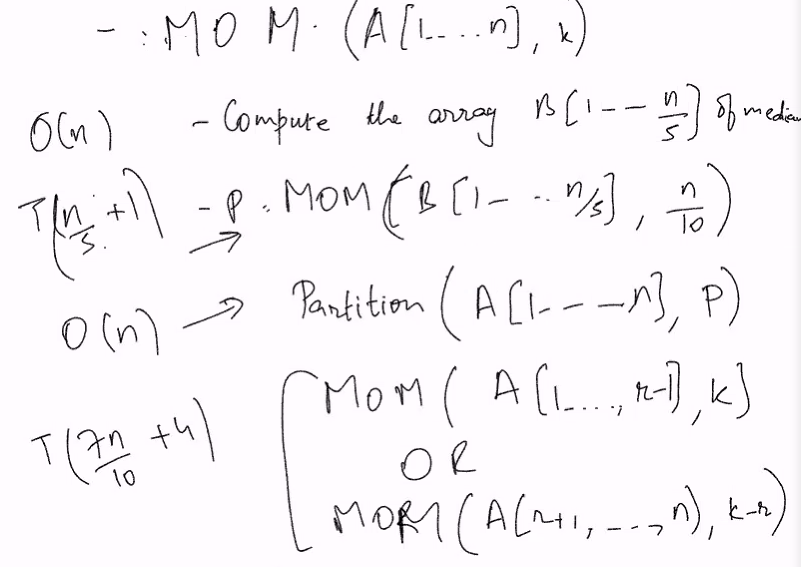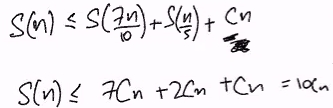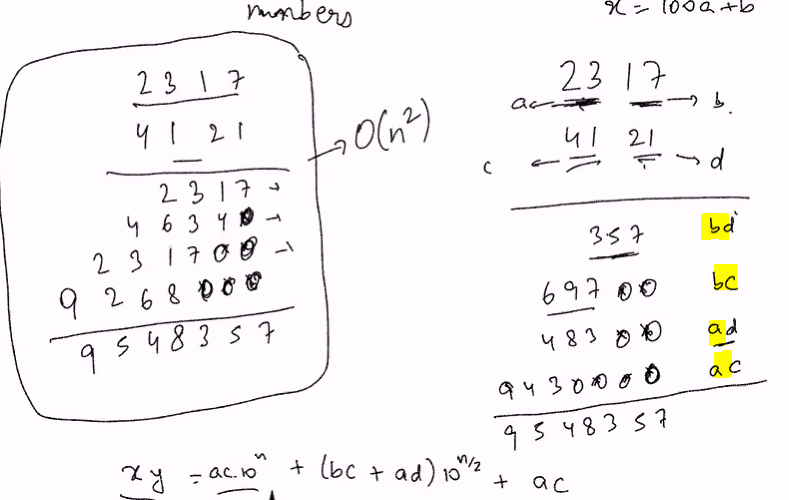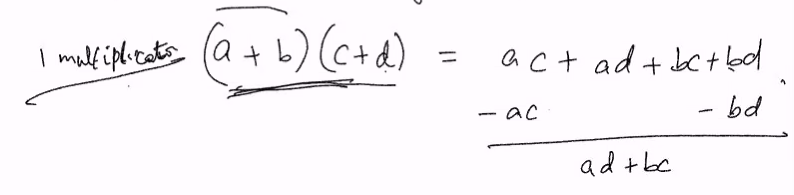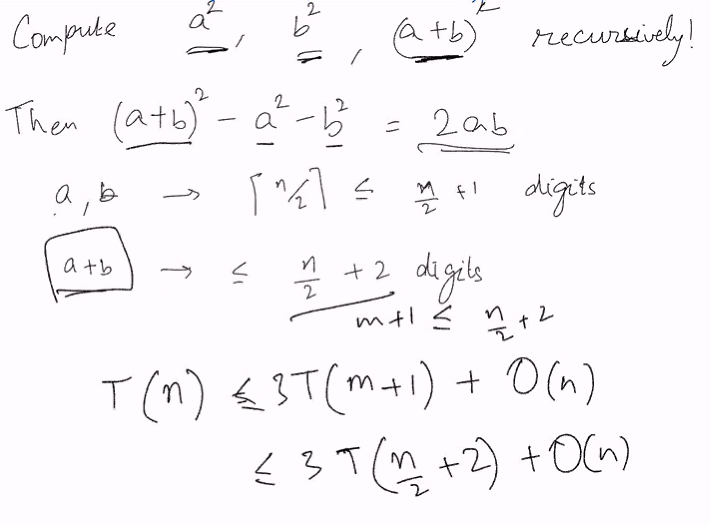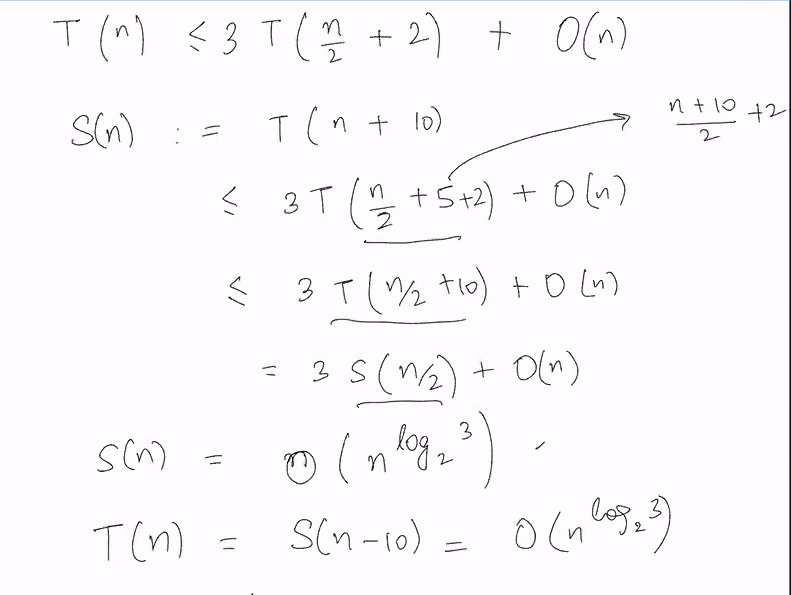Handling recursion

Simplify and delegate

1. If instance can be solve directly, then solve directly
2. Else, Reduce it to one or more simpler instances of exactly the same problem e.g In an algorithm for Squaring a number, one cannot make a recursive call to a multiplying two integer b and c
3. Imaging someone will solve the simpler problem
4. Base case

Key step

• Divide/Reduce the problem
• Recursively obtain solution of smaller instances
• Combine recursive calls and obtain final output

BASE CASE IS IMPORTANT!

Examples of recusive algorthim

• Mergesort
• Quicksort
• Binarysearch

Mergesort

Quicksort

• Choose a pivot
• Put the elements smaller than pivot one side of the pivot and the rest the other side
• Partition takes linear O(n) time
• Recusively sort O(logn)

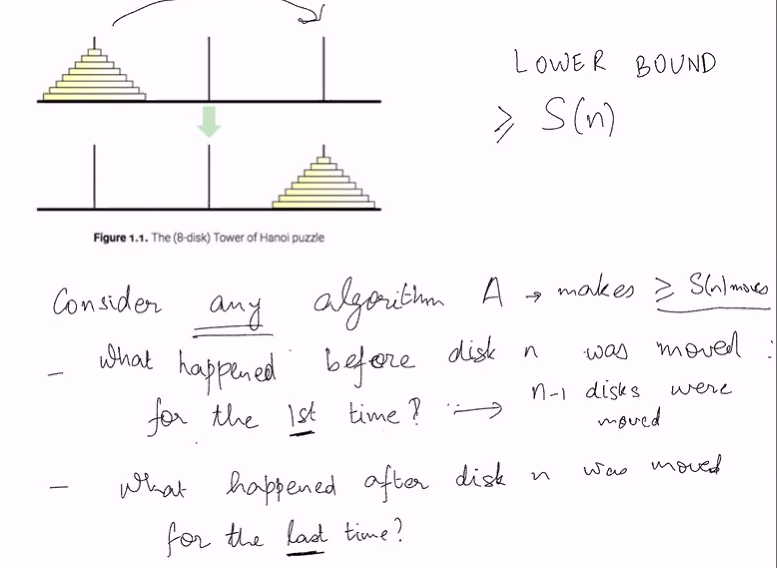
Tower of Hanoi

Conditions:

• Smaller disk must always be above the larger disk
• Move one disk at a time

In the recusive solution, we move the first n-1 disk into rod 2, then move the final disk from 1 to 3 before moving the n-1 disks from 2 to 3

There exist no other algorithm that takes faster than this

• There must have been a step where the largest disk was moved for the first time
• But before moving this, we need the top n-1 to move to rod 2 from rod 1
• Once the largest disk was moved to 3 for the last time, n-1 must have all move from which ever rod they were on to rod 3

S(n) is the minimum possible number of steps for moving n disk from rod 1 to another rod

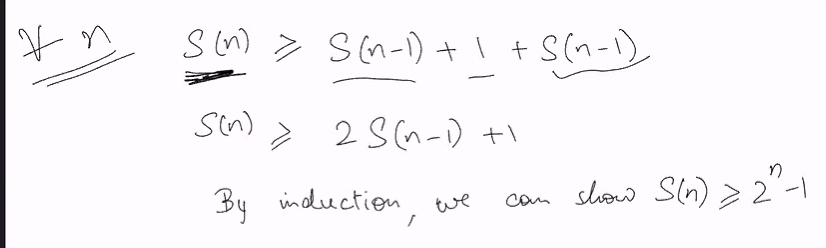
S(n) >= 2S(n-1) + 1 :

• Looking at the must move..
  • S(n-1): Move the top n-1 from rod 1 to 2
  • • 1 : Move the bottom largest disk
  • • S(n-1): Move the top n -1 disk from rod 2 to 3

Lower bound for TOH: Min no os steps requried for any algo that solves TOH

Lower bound for algo A: Min no of steps required by Algo A: 2^n -1

TO show that the algo is fastest is to show that the algo is the minimum number of steps to solve it

In conclusion, we cannot do better than T(n) = 2T(n-1) + 1, meaning that your algorithm can only be this or slower.

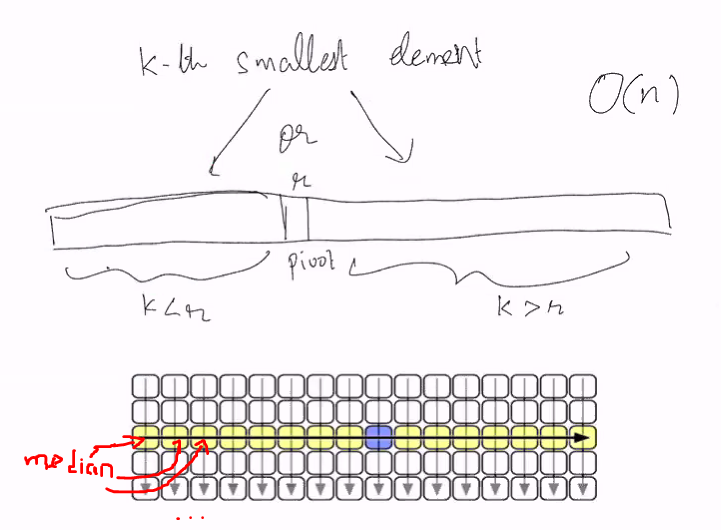
Linear Time selection

Find the medium of A (an array) recursively

Define a more general problem of finding the kth smallest element

• Use a variant of quick sort “Quick select”
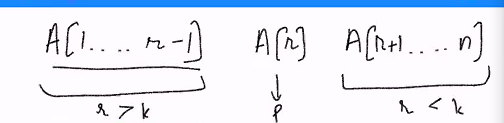
  • Takes the pivot (r)
  • Check if r < k
  • If r is less than k, then it shld be on the left else the right

The worst case would be if the pivot is either the smallest or the largest element in the array in which case the running time is O(n^2)

Good pivot

• a: the ratio for the next pivot within that block where a<1

Use master theorem and induction to prove that this solve to T(n) = O(n)

Our goal is to find a set of elements of size for some constant a<1 in O(n) time such that this set contains the kth smallest element

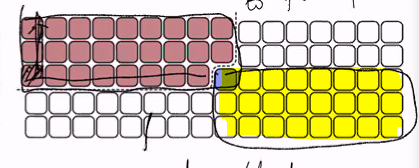
Compute the MOM (median of medians) recusively (The blue box), this is a very good pivot

In this image, the red boxes are smaller than MOM while the yellow is larger than MOM

We want the rank to not be too close to n nor 1

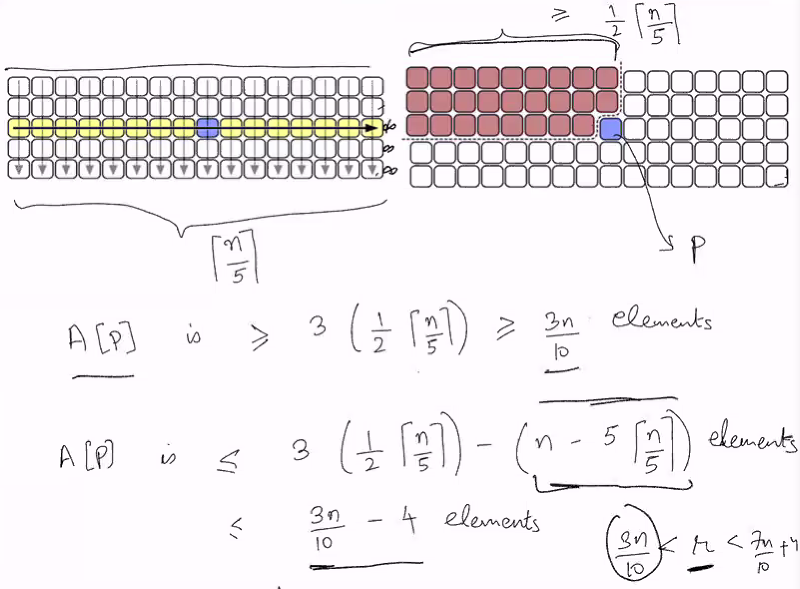
• 7n/10 + 4 : upper bound
• n/5 + 1 : MOM
• n: Partitioning from 1 - n with p values

MOM is smart quick select

MOM(A[1..N]):

• Compute the array B[1..n/5] of medians O(n)
• Make a recusive call p = MOM(B[1..n/5],n/10), this is the blue element in the pic O(n/5 +1)
• Partition the pivot(A[1..n], p), which will create a MOM(A[1..r-1], k) or MOM(A[r+1...n], k -r) depending on if k < r. r is the rank of the pivot O(7n/10 + 4)

It partition the n element into blocks of 5 and compute the median of these blocks. This will give us n/5 medians. We will take the middle elements out of these 5 (Recusive call with A array replaced by B), choose the pivot. Partition A using the P we got and we will do normal quick select where if k<r, we will parition from 1 to r-1 else r+1 to n

• The 4 is to make it a multiple of 5, in this example we want to assume n is a multiple of 5

Domain transformation

We sub in a random number (Which explains the 20 in img)

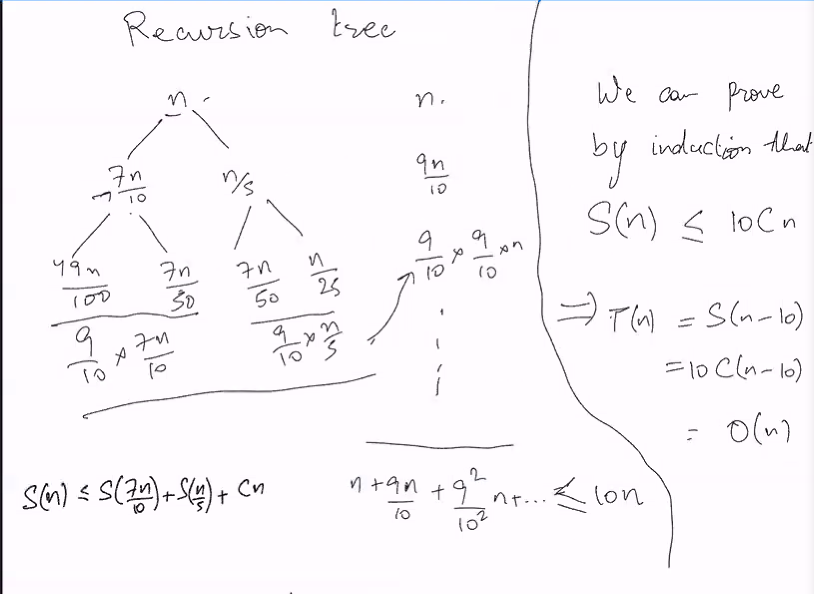
We realised that the sum of the children is 9/10..

• Recusive call to quick select from one side
• Recursive call to find the pivot using quickselect (MOM)

This is a geometric series of n/(1-0.9) = 10n thus we can guess that S(n) <= 10Cn, using induction we can prove this

We want to achieve O(n) but we got T(7n/10 + 4) + T(n/5) + O(n) which is still ok

Quick select with MOM paper

It cannot be groups of 3 because it does not help us prove linearity.. it will give us O(nlogn) instead.

Integer multiplication

• Algorthim for multiplying two n digit integers requires n^2 multiplication and O(n) addition so it runs in O(n^2)

• x = a.10^m +b
• y = c.10^m +d

x.y = ac.10 ^ (2m) + (ad+bc) 10 ^m + bd

We want ac, bd , ad+bc

Algo 1: Recursively compute ac, ad, bd , bc => 4 multiplcation recursive calls

Algo 2:

Using a clever trick by split multiplcation: We only need 3 m digit numbers

• Multiply(a,c)
• Multiply(b,d)
• Mulitply(a+b, c+d)
  • Multiply(a,c)
  • Multiply(b,d)

This will give us T(n) = (ceil(n/2) + 1) + O(n) = 3T(n/2 + 2) + O(n), using master theorem

Remove the ceil by overestimating 1

Compute x^2

x = 10^m a + b where a,b are m digit numbers and m = ceil(n/2)

Compute a^2, b^2 and (a+b)^2 recusively

Slides