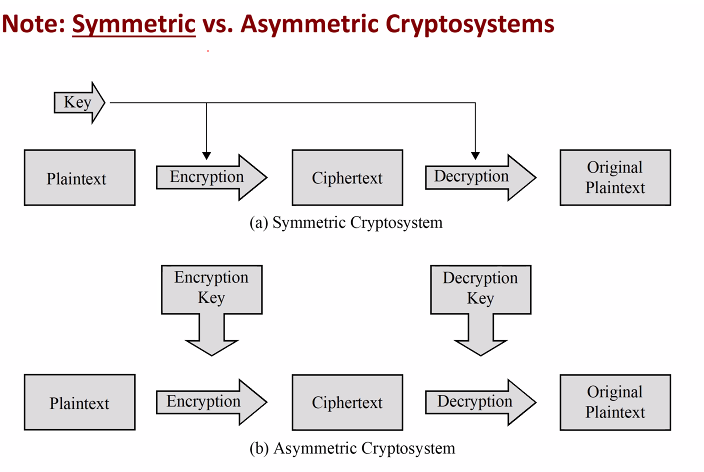
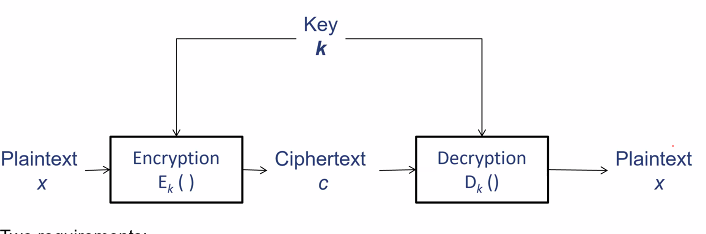
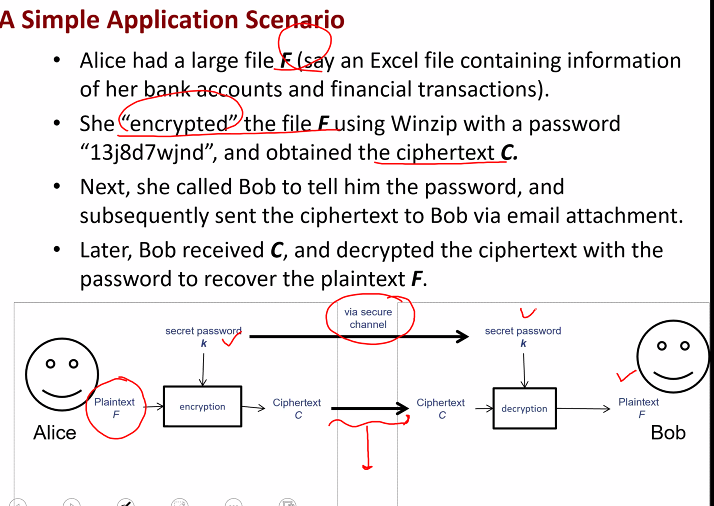
Encryption

An encryption scheme also known as cipher consist of encryption and decryption.

Requirements:

• Correctness: For any plaintext x and Key, D(E(x)) = x
• Security: Given the ciphertext, it is difficult to derive usefull infomation of the key and plain text
• Performance requirements: Efficiently computed

Example

Cryptography

Cryptography is the study of techniques in securing communication in the present of adversaries.

Encryption is one of the basics of cryptography

Applications:

• Secure communication/transaction
• Disk Encryption
• Content protection
• Password
• Digital signature
• Cryptocurrency: E.g Bitcoin

Charactersin Cryptography

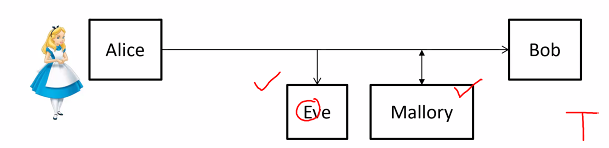
• Alice: Originator of message
• Bob: Recipient
• Eve: Eaves dropper, listen to sent message
• Mallory: Mallicious and modify message

  Sometimes these characters might not be human

Classical cipher

Substitute Cipher

Its just mapping a value to another value

Some terms:

• The key space: The set of possible keys
• Key space size: The total number of possible keys
• The key size or key length: The number of bits required to reperesent a particular key
• For subsitution ciper:
  • The key space
  • The space size : 27!
  • The key size : log2(27!) = 94 bits

The key is the a,b,c

This is called a trivial key, it is a trivial permutaion

Encryption/Decryption

Attacks on cipher

• Attacker goals is to
  • find the key: If found, the cipher is broken
  • To obtain some info about the plaintext
• Before commencing an attack, the attacker needs to access to some info such as:
  • A large number of ciphertexts that are all encrypted using the same key “Ciphertext only” or
  • Pairs of cuphertext and the corresponding plain text, “known plaintext”

Exhastive search (brute force) attack

• Search the key : Examine all possibble keys one by one
• Exhastive search is infeasible normally
• For some moden cipers like DES, it is feasible to break it using exhastive search
• Sophisticated attacks exploit the properties of the encryption scheme to speed up proccess, “analytical attacks”

Example: Known plain text scenario

• Consider the substituition ciper of size 27
• Attacker has access to ciphertext c and plain text X
• Let S be set of all possible subsitiution table

It will take very long because we are trying for each permutaion of table

• Running time depends on size of key space S
• On avg: 2^93 loops

Better attack on known plain text

• Attacker can figure out the entries in the key as long as given a plaintext and cipher text
• If the attacker has access to pais of ciphertext and their corresponding plaintext, they can guess the key
• Substitution ciper is insecure under known plaintext attack

** SUBSTITUTION CIPHER IS INSECURE **

Remarks

• There is requirement to know the corresponding plaintext
  • Attacker does not need to know the full plaintext but only the first few bytes of the plaintext are enough
• Guessing:
  • Email data: certain words in its header are fix e.g “from”
  • Many network protocol with fix headers
  • Commonly used words like “Weather” and “Nothing to report”

Exhastive search: Ciphertext only

• Only have ciphertext
• Knows plain text are english sentence

• Evantually will find the key
• There is small probability that the above algo finds a wrong key
• For sufficiently long cipher text, the probability that a wrong key will give meaningful english setence is v low.

They can map frequently occuring letters to the ciphertext to the frequently occuring letters of english

Shift and Caesar ciphers

• Shift Cipher: A type of sub cipher
• Each letter in plaintext is shifted a certain number of places down the alphabet
• Example (shift by 1):
  • A would be replace by b
  • B become C
• Caesar cipher:
  • SHift with 3
  • If no key. 3 is the key

Key space: 27

Vigenere Cipher

It is a polyalphabetic cipher

• Uses a keyword instead of a single shifting distance in shift cipher: A string of letters representing numbers based on their position in the alphabet
• Example: “SOC” = 18, 14, 2
• They keyword get repeated for a longer plaintext
• Keyword is used to select which shifting distance to be used for each letter of the alpha
• Tabula recta

Security

• Weak against known plaintext attack
• Not that weak agaisnt cipher only attack (Need find good attack technique)

Suppose we know k = length/period of the keyword

Obv: All letters of the plaintext whose index is i (mod k ), for i = 0..k-1.. get shifted by the same key character. We can use frequency analysis technique and this cipher turns into a monoalphabetic ciper again

• Kasiski method:
  • Repetition in the cipher text give clues to period
  • Having the same letter block at period apart result in the same letter block in the cipher text
  • Example: WBLBXYLHWBLWYH
  • Period: 9 (From the start to the next start)
  • Hence if we find repeated pattern with distance m, guess the period k where k/m

Period is 1/Frequency

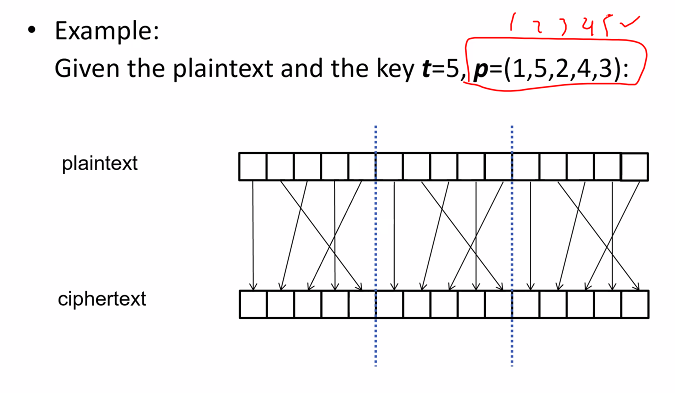
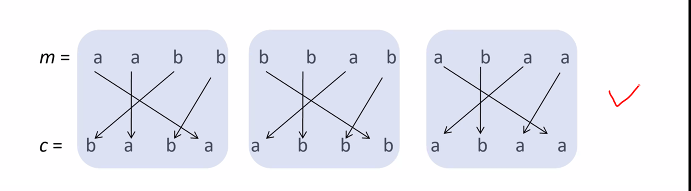
Permutation Cipher

Known as transposition cipher

• Group plaintext into blocks of t characters
• Apply a secret “permutation” to the character in each block by shuffeling the character
• the block size t would be part of the key: t shld be kept secret

Known Plaintext

• Fails miserably in this
• Given plaintext and ciphertext, it is very easy to determine

Ciphertext only attack

Permutation cipher can be broken easily if plaintext is an english text

One time Pad

The key is random generated Encryption and decryption process is the same

Example

x is plaintext, k is key

Security

• From a pair of cipher and plain: Yes, can derived
• But key is only one time use
• It is not clear how to apply exhastive search on one-time pad
• One time pad leaks no info of the plaintext except its lenght even if the attacker has an arbitraru running time
• One time pad is called “unbreakable” (Due to the random secrecy)

every single letter has the same probabbility

Remarks

• Key must be at least as long as the message

Cyptosystem

• More formally defined as algo (G, E, D) over sets (K, M, C):
  • K: Set of all keys (Key space)
  • M: Set of all plaintext
  • C: Set of all ciphertext
  • G: Generates k, key generation algo
  • E: Encruption algo
  • D: Decryption ALgo
• Requirements
  • Correctness: For all m in M and k in K, output by G, D(E(m)) = m
  • Efficient: G, E, D, Fast generation
  • Security: Attackers cannot recover the secret key or plaintext
• Perfect security/Secrecy: Regardless of any prior infomation that attackers has about plaintext, the ciphertext should leak no additional infomation about the plaintext

Questions to ask:

• Is it unnecssarily strong for praticial usage
• Any security notion that is more relaxed and practical

Security Gurantee: Computational secrecy

• More relax
• Infomatlly : Still fine if cipher leaks some info with tiny probability
• Impacts:
  • Security may fail with tiny probability
  • Agaisnt computationally bounded attackers: - If one key is tested per clock cycle, a supercomputer can check 2^80 keys per year - A super computer since big bang can check ~2^112 keys - Key space size of modern ciphers >= 2^128

Computational assumption is important:

• Enable proof of security
• Implication if assumption is proven wrong
• Allows for some meaningful comparision of different ciphers

Exhastive search and key length

• See work factor

• Quantify the security of an excryption scheme by the length of the key

• Some schemes such as RSA have known attacks that are more efficient that exhastively searching all the keys
• In those cases we want to quantify the security by the equivalent exhastive search

Security analysis of cipher

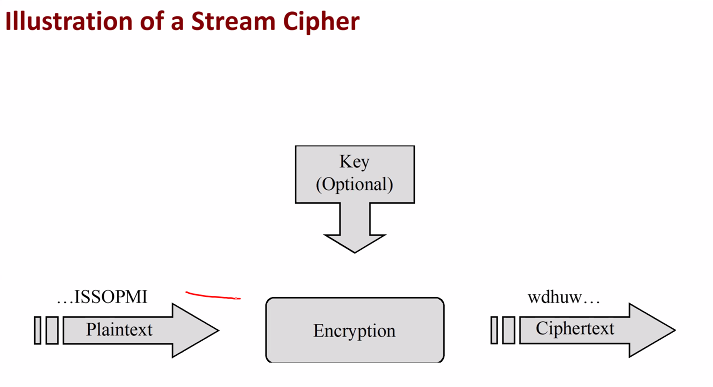
Modern ciphers

Modern ciphers generally refers to schemes that use computer to encrupt and decrypt

Sym key based modern ciphers: Stream cipher and block cipher

Designs of modern cipher consider known sttacks:

• DES
• RC4
• A5/1
• AES
• A5/3

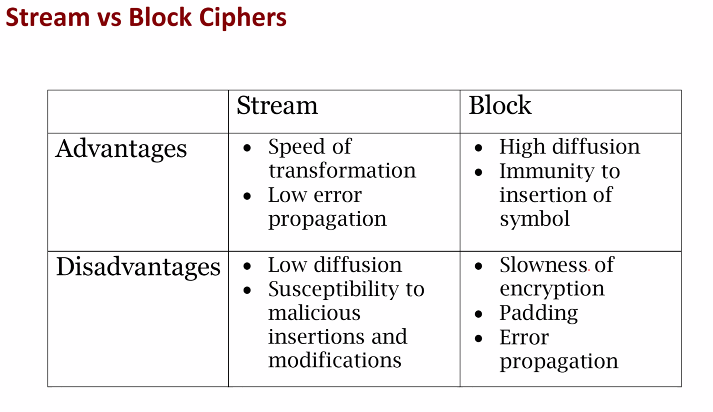
Steam vs Block

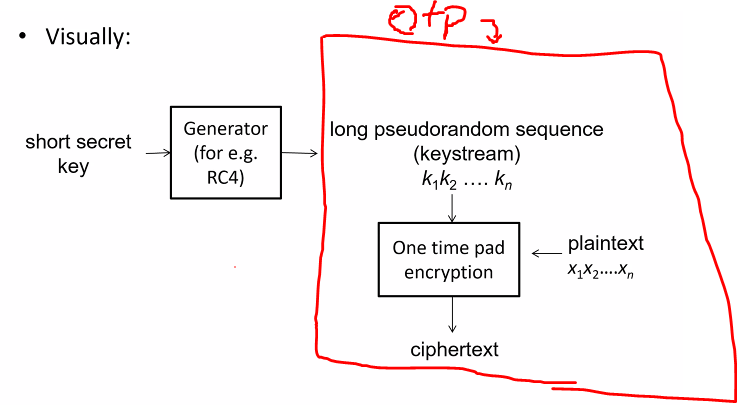
Steam cipher

Inspired by one type pad

• Suppose the plaintext is 2^20 bits, but key is only 256 btits
• Steam cipher generates a 2^20 sequences for the key and takes the generated sequence as the secret key in one time pad
• Pseudorandom sequence is called keystream sometimes

Pseudorandom Generator

• The security of a stream cipher relies on use generator
  • PRG: Psudorandom generator
  • PRNG: Pseudorandom number generator
• Prop:
  • PRG: Maps the seed space to the output space deterministcally and efficiently
  • Selector seed must be random
• Useful when we have small num of true/good random bits and wants a lot of random looking bits

Issues: Same seed generates the same keystream (Two key issye in one time pad)

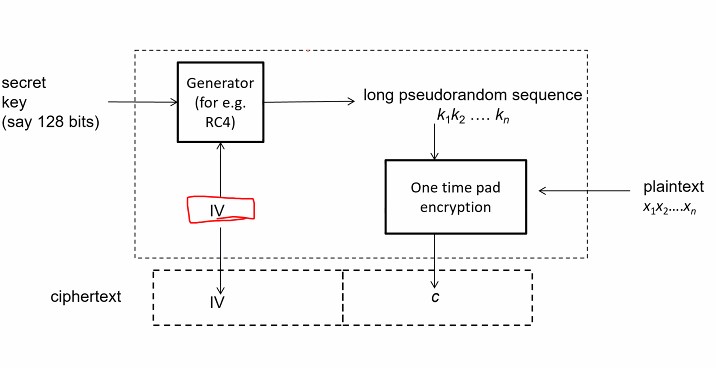
Solving the two key issue: Steam cipher with initial value (IV)

Focus on IV:

• We need to make the generator randomnised
• IV is part of the cipher text

For decryption, IV can be extracted from the ciphertext.

Why IV?

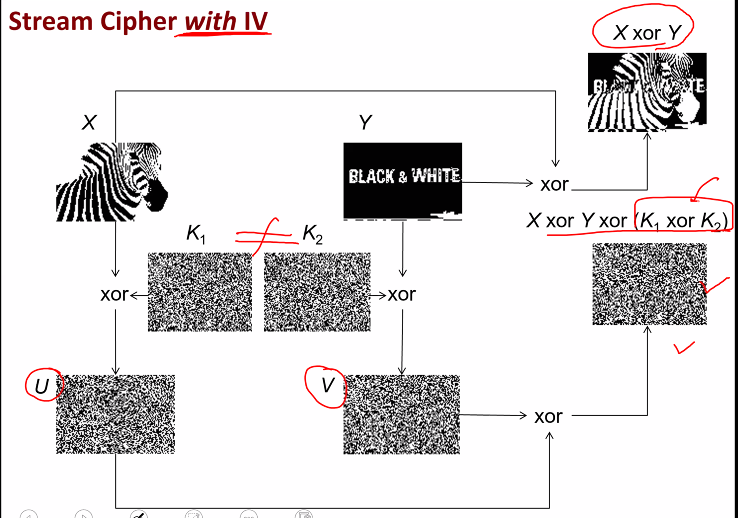
• Suppose there is no IV, IV is set to a string of 0
• COnsider the situation where the same key is used to encrupt two different plaintext:
  • X: x1x2x3 and
  • Y: y1y2y3

This is similiar in asking why the key must be random each time

Revealing X xor Y

Without IV:

With IV:

• IV are likely be different
• 2 Pseudorandom sequences are thus likely to be different
• The ciphertexts are also likely to be different

Slide