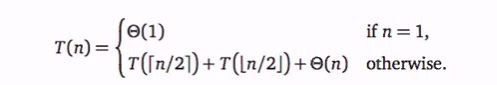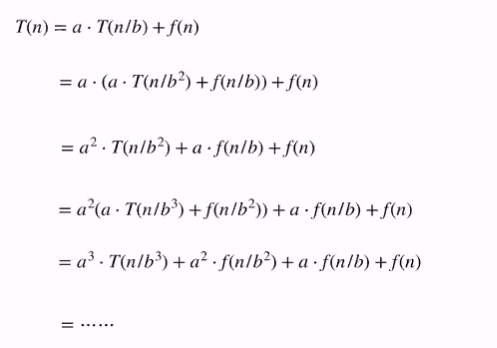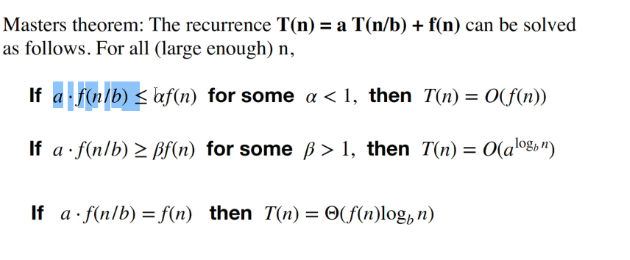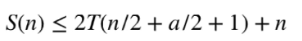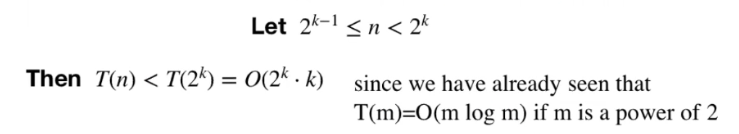Time complexity

  • worse case and average:
  • Worse: Max time that is required with input size n
  • Avg: Assume that input is distributed somewhere randomly

Assume the finite set of inputs, we consider only contains two inputs, A1 and A2. The time needed for solving them is T1 and T2. Avg time is (T1+T2)/2

Asymptotic time complexity

Look at the term that grows the fastest and ignore the constant

e.g f(n) = 39m^2 +16n +5

  • We will only look at n^2

Why ignore?

  1. Growing factors are more significant
  2. The cosntant is usually small for most algo

Upper and lower bounds

1-1.PNG

We can say that as n tend to infinite, f(n)/g(n) <= C

Recurrence relation

Analysisng how long the algorithms takes.

Max search example

3230-1-7.PNG

This is a recursive algo

  • Compares the max element with the max of the past largest elements using recursion

Binary search example

3230-1-8.PNG

Convention

T(n/a) means T(floor(n/a))

Proving asymptotics using limits

3230-1-1.PNG

  • Compute the ratio as n tends to infinite.

3230-1-2.PNG

Solving recurrence relation

Induction

Try to guess a close form solution

  1. Compute value of the function at a few points
  2. Unfold the recurrence a few steps

Try to prove by induction after making a guess.

3230-1-3.PNG 3230-1-4.PNG

We have to proof k+1, in this example, they use n and n-1

3230-1-9.PNG

3230-1-5.PNG

We can open up to find the pattern

Mergesort

3230-1-11.PNG

  • Mergesort recursively left and right
  • Merge (linear) current

3230-1-10.PNG

3230-1-12.PNG

We open up and make a guess, after that we will use induction to prove it.

  • Plug in the bound and we will prove that it is nlogn for big O and omega

Recursion trees (Divide and conquer)

T(n) = aT(n/b) +f(n)

We can open this recursion to get:

3230-1-13.PNG

We can take note that the number of variables is increasing

3230-1-14.PNG

F(n) is the additional number of steps needed

Master theorem

Partition into 3 different cases, if one is solve.. can solve the rest with the same way. Try to fit the recurrence into this fomula

3230-1-6.PNG

Using geometric series of a/1-r where 1-r is constant, we can ignore the 1-r and we will just get a -> O(a)

Transformations

Sometimes we might not be able to apply our methods for solving recurrence relation directly. Thus we transform it such that we can apply our methods

  • Domain: S(n) = T(g(n)) for some appropriatey chosen function g
  • Range: S(n) = g(T(n)) for some appropriately chosen function g

Example: Unsimplified merge sort

Given a recurrence relation of merge-sort:

3230-1-15.PNG

We can overestimate to: 3230-1-16.PNG

Our goal is to get a standard form of: S(n) < = 2S(n/2) + n, so we make the transformation of S(n) = T(n+a)

We get: 3230-1-17.PNG

Notice we can get the desire form if a=2

Alternative

  • Domain substitution is not really necessary

3230-1-18.PNG

= O(2nlog(2n)) = O(nlgn) since 2^k <= 2n

Example

T(n) = T(n/2) + T(n/4) +1

This reccurence doesnt seem to fit any of our known techniques. Using trial and error suggest that using domain transformation would convert it to look nicer

  • Taking n = 2^k
  • We will get t(k) = T(2^k)
  • Substituting it we will get t(k) = t(k-1) + t(k-2) + 1
  • This is a fib recurrance.

We can get the exact form by making range transformation (k) = t(k) + 1 to get

s(k) = s(k-1) + s(k-2)

We solve s(k) before solving t(k) then solving T(k)

What ever transformation we did, we need to change back

Slides