CS2100: Simplification

To get simpler expression for fewer logic gate.

-> Cheaper

Use theorems

Open ended requires skills

- Reduce number of literals

- Reduce number of terms

Sometimes these conflict, reducing one does not mean reduce the other

Focus on reduce literals by using the laws.

Easy to use

Limited to no more than 6 variables

But we need truth table:

Make it to a sum of products, find everything that includes the answer

1. For each 1 in kMap, draw the largest possible group in power of 2

Draw the prime implicants

2. Take all groups that cover unique 1

Take all Essential Prime implicant

3. For any remaining 1, not cover by groups

Choose the smallest collection of prime implicant for the rest that were not covered in 2

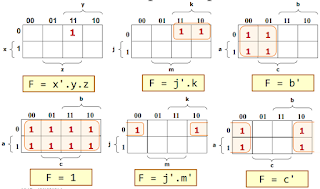
Reading it:

See the intersection

If everything is 1, it is just true

Generalised

Group 1 : 0 literals

Group 2: 1 Literals

Size X : log(2) X literals

[Practice Here : 1.16]

Implicant:

A produce term that could be use to cover several minterms of the function

-> The 1 in the boxes

Prime Implicant:

Maximal Possible implicate for a group of minterms

Essential Prime Implicant:
Prime implicant that contains 1 or more unique minterm

Find the F prime

=> Flip all the 0 and 1 from the original k-map

We use this to get the demorgon rule

(Or just do kmap on the 0s for original k-map if we are good)

The output can be 1 or 0.

e.g ABCD represents a digit, counts whether there are even numbers of 1 in the binary representation

Use x to indicate a don't care condition.

These don't care condition can be use to simplify the expression easily.

Use sumD(10,11,12,13) to show the dont care.