MIPS Introduction

We can retrieve the assembly code by running this command on a c prog
-> gcc -s hello.c
//this will generate a .s file which is the assembly code
vim hello.s


Execution walkthrough

1. Read
2. Process Figure/ decode
3. Fetch oprands
4. Execute
5. Storeback

However, memory access is slower than process speed thus we have to avoid memory storage by using temp register to store
Most processor now is at least ten times faster than the memory access
This is bad as processor would wait for the memory to access.

Memory Instruction

Will move the memory into the register, this is to help with the time wasted in memory access
e.g load, store

Reg-to-Reg Arithmetic

Arithmetic operation only works on register, memory wont be touched

The ALU will do the calculation

Loop

Execute commands from top down.
To loop, we check a condition and if condition is true,
we jump back to the tag indicated

Summary:
Both instruction and data are stored in memory
Limit memory access

MIPS Assembly Language

General Purpose Register

- Registers are useful as it helps access memory faster.
Data are transferred from memory to register for faster processing.
However, there are limited number of registers.

- Registers have no data type
Machine/Assembly instruction assumes data is correct type

Types of registers
$zero - Only stores 0, cannot be changed
$t0 - $t7 (8-15) - Temp for storing
$s0 -$s7 (16-23) - program variables
$t8 - $t9 (24-25)- Temp for Calculation

We can reference the register by number or by the names.

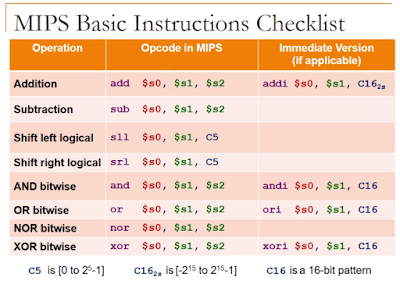
Arithmetic Operation

Addition:

a = b + c

add $s0, $s1, $s2

This is called variable mapping.
The value is map into the register.

However. Order is important

Subtraction:

a = b - c

sub $s0, $s1, $s2

$s1 -> b
$s2 -> c

Note:
For complex expression such as 
a = b - c + d
We can split it to multiple assembly codes.
Since + and - lies on the same precedence,
we evaluate left to right

Constant/ Immediate Operands

addi:

To add a constant to a number we use addi

a = a+ 4

addi $s0, $s1 , 4
However, the constant can only range from -2^15 to 2^15 - 1
Which is 16 bit 2s complement

Register Zero:
f = g

We can just run

add $s0 , $s1 , $zero

Pseudo-Instruction

move $s0, $s1

is similar to 

add $s0 , $s1 , $zero

Logical Operation

Nor is not (A or B)
Xor is exactly One



Shifting

We use shifting to move the bits
This is useful for multiplication.

By moving 4 bits to the left, its equivalent to multiplying x2^4

Shifting to the right will divide instead.


And Operator

Using the logical operations to get the bits we want (Masking)


Or Operator
- We force certain bits to 1s.

Nor Operator

- We can use this to not since there is no not operator
To not it, just apply a 0 to not the answer.

nor $t0, $t1 , $zero
Where $t1 is the bit that we want to not

XOR Operator

If both bits are the same, return 0
If both bits are different. return 1

We can do a not for xor bit by applying a 0xFFFFFFFF

Load upper immediate

- LUI to set the upper 16 bit
- Set the lower bits as 0

Or Immediate

- Apply to set lower order bits







<Prev               Next>